
���κ��� ��ͼ����ͼ����A0λ������ԭ�㣬��A1��A2��A3��An��y����������ϣ���B1��B2��B3��Bn�ڶ��κ���λ�ڵ�һ����ͼ���ϣ���C1��C2��C3��Cn�ڶ��κ���λ�ڵڶ�����ͼ���ϣ��ı���A0B1A1C1���ı���A1B2A2C2���ı���A2B3A3C3���ı���An��1BnAnCn�������Σ���A0B1A1=��A1B2A2=��A2B3A3��=��An��1BnAn=60�㣬����An��1BnAnCn���ܳ�Ϊ ��
��ͼ����ͼ����A0λ������ԭ�㣬��A1��A2��A3��An��y����������ϣ���B1��B2��B3��Bn�ڶ��κ���λ�ڵ�һ����ͼ���ϣ���C1��C2��C3��Cn�ڶ��κ���λ�ڵڶ�����ͼ���ϣ��ı���A0B1A1C1���ı���A1B2A2C2���ı���A2B3A3C3���ı���An��1BnAnCn�������Σ���A0B1A1=��A1B2A2=��A2B3A3��=��An��1BnAn=60�㣬����An��1BnAnCn���ܳ�Ϊ ��

 â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱������ɽ�����꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��֪���������� ��ͼ������ÿһ��֧�ϣ�y��x���������С����˷����������Ľ���ʽ������ ����ע��ֻ��д��һ����ȷ�𰸼��ɣ�
��ͼ������ÿһ��֧�ϣ�y��x���������С����˷����������Ľ���ʽ������ ����ע��ֻ��д��һ����ȷ�𰸼��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱����˳�������꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��֪������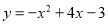 ����1�������������ߵĶԳ���Ͷ������ꣻ��2���ڸ���������ϵ�л�����������ߣ�����������x�ύ��A��B���㣬��y�ύ�ڵ�C�����ABC�������
����1�������������ߵĶԳ���Ͷ������ꣻ��2���ڸ���������ϵ�л�����������ߣ�����������x�ύ��A��B���㣬��y�ύ�ڵ�C�����ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱����ʯ��ɽ�����꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��ͼ1����Rt��ABC�У���ACB=90�㣬��B=60�㣬DΪAB���е㣬��EDF=90�㣬DE��AC�ڵ�G��DF������C��
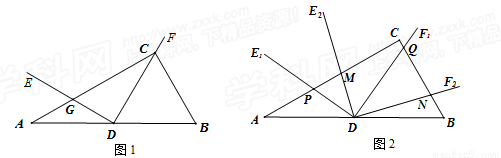
��1�����ADE�Ķ�����
��2����ͼ2����ͼ1�еġ�EDF�Ƶ�D˳ʱ�뷽����ת�� ��
�� ������ת�����е���������λ�÷ֱ��Ϊ��E1DF1����E2DF2 �� DE1��ֱ��AC�ڵ�P��DF1��ֱ��BC�ڵ�Q��DE2��ֱ��AC�ڵ�M��DF2��ֱ��BC�ڵ�N����
������ת�����е���������λ�÷ֱ��Ϊ��E1DF1����E2DF2 �� DE1��ֱ��AC�ڵ�P��DF1��ֱ��BC�ڵ�Q��DE2��ֱ��AC�ڵ�M��DF2��ֱ��BC�ڵ�N����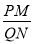 ��ֵ��
��ֵ��
��3����ͼ1�С�B=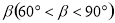 ����2���е������������䣬�ж�
����2���е������������䣬�ж�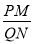 ��ֵ�Ƿ�Ϊ��ֵ������ǣ���ֱ��д�����ֵ���ú�
��ֵ�Ƿ�Ϊ��ֵ������ǣ���ֱ��д�����ֵ���ú�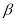 ��ʽ�ӱ�ʾ����������ǣ���˵�����ɣ�
��ʽ�ӱ�ʾ����������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱����ʯ��ɽ�����꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
һ�κ��� 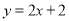 �뷴��������
�뷴��������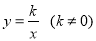 ��ͼ����A
��ͼ����A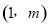 ��
��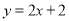 ��ͼ����
��ͼ����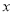 �ύ�ڵ�B��
�ύ�ڵ�B��
��1�����B���꼰�����������ı���ʽ��
��2��C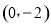 ��
�� ����һ�㣬���ı���ABCD��ƽ���ı��Σ�ֱ��д����D�����꣬���ж�D���Ƿ��ڴ˷�����������ͼ���ϣ���˵�����ɣ�
����һ�㣬���ı���ABCD��ƽ���ı��Σ�ֱ��д����D�����꣬���ж�D���Ƿ��ڴ˷�����������ͼ���ϣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱����ʯ��ɽ�����꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
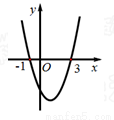
��֪�����κ���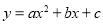 ��ͼ����ͼ��ʾ������˵������ȷ���ǣ� ��
��ͼ����ͼ��ʾ������˵������ȷ���ǣ� ��
A��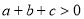
B��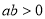
C��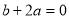
D����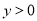 ʱ��
ʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱���к��������꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��ƽ��ֱ������ϵxOy�У����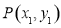 ��
��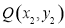 ��ͼ��W�ϵ��������㣮
��ͼ��W�ϵ��������㣮
����ͼ��W�IJ���������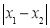 �����ֵΪm��
�����ֵΪm��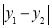 �����ֵΪn����
�����ֵΪn����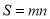 Ϊͼ��W�IJ�������
Ϊͼ��W�IJ�������
���磬��ͼ��W�ǰ뾶Ϊ1�ġ�O����P��Q�ֱ��ǡ�O��x��Ľ���ʱ����ͼ1��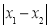 ȡ�����ֵ�������ֵm=2����P��Q�ֱ��ǡ�O��y��Ľ���ʱ����ͼ2��
ȡ�����ֵ�������ֵm=2����P��Q�ֱ��ǡ�O��y��Ľ���ʱ����ͼ2��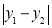 ȡ�����ֵ�������ֵn=2����ͼ��W�IJ�����
ȡ�����ֵ�������ֵn=2����ͼ��W�IJ�����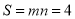 ��
��
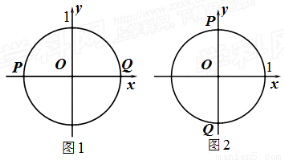
��1����ͼ��W�ǵ���ֱ��������ABO��OA=OB=1��
����ͼ3������A��B����������ʱ�����IJ�����S= ��
����ͼ4����AB��x��ʱ�����IJ�����S= ��
��2����ͼ��W��һ���߳�Ϊ1��������ABCD�����ͼ�β�����S�����ֵΪ ��
��3����ͼ��W��һ���߳��ֱ�Ϊ3��4�ľ���ABCD�������IJ�����S��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱���к��������꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ����֪����ABCD�ij�ABΪ5����BCΪ4��E��BC���ϵ�һ�����㣬AE��EF��EF��CD�ڵ�F����BE=x��FC=y�����E�ӵ�B�˶�����Cʱ���ܱ�ʾy����x�ĺ�����ϵ�Ĵ���ͼ���ǣ� ��
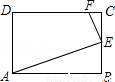
A�� B��
B��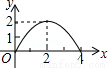 C��
C��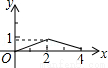 D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱���ж��������꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��ͼ���ڡ�ABC�У�AB=AC=8��BC=6����DΪBC��һ�㣬BD=2������D������DE��AC�ڵ�E��ʹ��ADE=��B�����߶�EC�ij��ȣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com