
【题目】如图,直线L: ![]() 与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.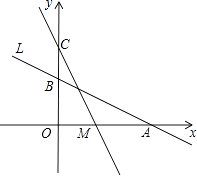
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.
【答案】
(1)
解:对于直线AB: ![]() ,
,
当x=0时,y=2;当y=0时,x=4,
则A、B两点的坐标分别为A(4,0)、B(0,2)
(2)
解:∵C(0,4),A(4,0)
∴OC=OA=4,
当0≤t≤4时,OM=OA﹣AM=4﹣t,S△OCM= ![]() ×4×(4﹣t)=8﹣2t;
×4×(4﹣t)=8﹣2t;
当t>4时,OM=AM﹣OA=t﹣4,S△OCM= ![]() ×4×(t﹣4)=2t﹣8
×4×(t﹣4)=2t﹣8
(3)
解:分为两种情况:①当M在OA上时,OB=OM=2,△COM≌△AOB.
∴AM=OA﹣OM=4﹣2=2
∴动点M从A点以每秒1个单位的速度沿x轴向左移动2个单位,所需要的时间是2秒钟;
M(2,0),
②当M在AO的延长线上时,OM=OB=2,
则M(﹣2,0),此时所需要的时间t=[4﹣(﹣2)]/1=6秒,
即M点的坐标是(2,0)或(﹣2,0)
【解析】(1)由直线L的函数解析式,令y=0求A点坐标,x=0求B点坐标;(2)由面积公式S= ![]() 求出S与t之间的函数关系式;(3)若△COM≌△AOB,OM=OB,则t时间内移动了AM,可算出t值,并得到M点坐标.
求出S与t之间的函数关系式;(3)若△COM≌△AOB,OM=OB,则t时间内移动了AM,可算出t值,并得到M点坐标.
【考点精析】根据题目的已知条件,利用一次函数的图象和性质的相关知识可以得到问题的答案,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ACB=90,AC=BC,点E、F在AB上,∠ECF=45,
(1)求证:△ACF∽△BEC
(2)设△ABC的面积为S,求证:AF·BE=2S

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(m+1)x+2m﹣6,
(1)若函数图象过(﹣1,2),求此函数的解析式.
(2)若函数图象与直线y=2x+5平行,求其函数的解析式.
(3)求满足(2)条件的直线与直线y=﹣3x+1的交点,并求出这两条直线与y轴所围成三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)的函数关系式,并求出自变量的取值范围;
(2)当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,O,B三点在同一直线上,∠BOD与∠BOC互补.

(1)试判断∠AOC与∠BOD之间有怎样的数量关系,写出你的结论,并加以证明;
(2)OM平分∠AOC,ON平分∠AOD,①依题意,将备用图补全;
② 若∠MON=40°,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的有( )
①对顶角相等;②两直线平行,内错角相等;③两个锐角对应相等的两个直角三角形全等④若a2=b2,则a=b;⑤若a>b,则ac2>bc2.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com