
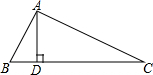
 如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )
如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 2 | D. | 3 |
分析 根据∠BAC=90°,AD⊥BC,得到∠BAC=∠ADC=90°,由于∠C=∠C,证得△ABC∽△ADC,得到比例式$\frac{AC}{BC}=\frac{CD}{AC}$,求得CD,根据勾股定理即可得到结论.
解答 解:∵∠BAC=90°,AD⊥BC,
∴∠BAC=∠ADC=90°,
∵∠C=∠C,
∴△ABC∽△ADC,
∴$\frac{AC}{BC}=\frac{CD}{AC}$,
∴AC2=BC•CD,
即(2$\sqrt{5}$)2=(1+CD)•CD,
解得:CD=4(负值舍去),
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{(2\sqrt{5})^{2}-{4}^{2}}$=2.
故选C.
点评 本题考查了相似三角形的判定和性质,勾股定理,熟练掌握相似三角形的判定和性质定理是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 100 | B. | 99 | C. | 99或100 | D. | 100或101 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 据媒体报道,近期“甲型H7N9禽流感”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“甲型H7N9禽流感”,对教室进行“熏药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示,第一段是线段OA,第二段是一个反比例函数的图象(即图中A点及其右侧的部分),根据图象所示信息,解答下列问题:
据媒体报道,近期“甲型H7N9禽流感”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“甲型H7N9禽流感”,对教室进行“熏药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示,第一段是线段OA,第二段是一个反比例函数的图象(即图中A点及其右侧的部分),根据图象所示信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 观察下面图形我们可以发现:第1个图中有1个正方形,第2个图中有5个正方形,按照这种规律变化下去…
观察下面图形我们可以发现:第1个图中有1个正方形,第2个图中有5个正方形,按照这种规律变化下去…查看答案和解析>>
科目:初中数学 来源: 题型:选择题
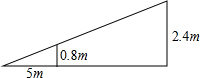 如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )
如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )| A. | 15米处 | B. | 10米处 | C. | 8米处 | D. | 7.5米处 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
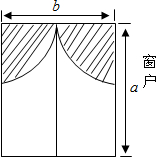 小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成:
小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com