
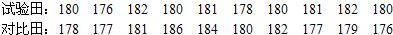
 试验=x′甲+180,
试验=x′甲+180, 对比=x′乙+180.
对比=x′乙+180. ×(0-4+2+0+1-2+0+1+2+0)=0(mm),
×(0-4+2+0+1-2+0+1+2+0)=0(mm), ×(-2-3+1+6+4+0+2-3-1-4)=0(mm).
×(-2-3+1+6+4+0+2-3-1-4)=0(mm). 试验=180(mm),
试验=180(mm), 对比=180(mm).
对比=180(mm). ×[42+3×22+2×12]=
×[42+3×22+2×12]= ×30=3;
×30=3; ×[62+2×42+2×32+2×22+2×12]=
×[62+2×42+2×32+2×22+2×12]= ×96=9.6.
×96=9.6. =
= (x1+x2+…+xn),即可求出数据x1+180,x2+180,…,xn+180的平均数.
(x1+x2+…+xn),即可求出数据x1+180,x2+180,…,xn+180的平均数. =
= (x1+x2+x3+…xn).方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为
(x1+x2+x3+…xn).方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为 ,则方差S2=
,则方差S2= [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.熟记公式是解决本题的关键.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.熟记公式是解决本题的关键. 

科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com