
阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值。
对于任意正实数a、b,可作如下变形a+b=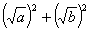 =
=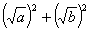 -
-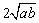 +
+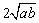 =
=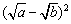 +
+ 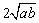 ,
,
又∵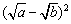 ≥0, ∴
≥0, ∴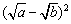 +
+ 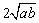 ≥0+
≥0+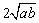 ,即
,即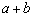 ≥
≥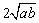 .
.
(1)根据上述内容,回答下列问题:在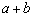 ≥
≥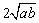 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥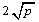 ,当且仅当a、b满足 时,a+b有最小值
,当且仅当a、b满足 时,a+b有最小值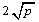 .
.
 (2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a,DB=2b, 试根据图形验证
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a,DB=2b, 试根据图形验证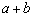 ≥
≥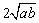 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.
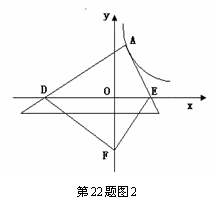
(3)探索应用:如图2,已知A为反比例函数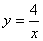 的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
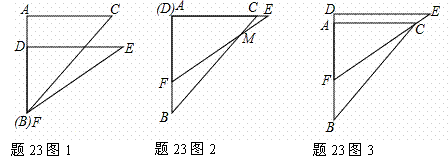
有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=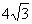 ,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上,现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动。
,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上,现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动。
(1)如图⑵,当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC= 度;
(2)如图⑶,在三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=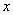 ,两块三角板重叠部分面积为
,两块三角板重叠部分面积为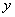 ,求
,求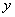 与
与 的函数解析式,并求出对应的
的函数解析式,并求出对应的 取值范围。(13南充卷改编)
取值范围。(13南充卷改编)
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
关于二次函数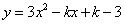 ,以下结论:① 抛物线交
,以下结论:① 抛物线交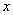 轴有两个不同的交点;②不论k取何值,抛物线总是经过一个定点;③设抛物线交
轴有两个不同的交点;②不论k取何值,抛物线总是经过一个定点;③设抛物线交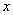 轴于A、B两点,若AB=1,则k=9;;④ 抛物线的顶点在
轴于A、B两点,若AB=1,则k=9;;④ 抛物线的顶点在 图像上.其中正确的序号是( )
图像上.其中正确的序号是( )
A.①②③④ B.②③ C.②④ D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、双曲线、圆,在看不见图形的情况下随机摸出1张,这张卡片上的图形既是中心对称图形又是轴对称图形的概率是( )(原创)
A.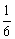 B.
B.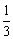 C.
C.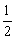 D.
D.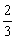
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com