
【题目】如图1,BC是⊙O的直径,A是⊙O上一点,过点B作⊙O的切线,与CA的延长线相交于点E,F是BE的中点,延长AF与CB的延长线相交于点P.
(1)求证:PA是⊙O的切线;
(2)如图2,若AD⊥BC于点D,连接CF与AD相交于点G.求证:AG=GD;
(3)在(2)的条件下,若FG=BF,且⊙O的半径长为![]() ,求BD的长度.
,求BD的长度.

【答案】(1)证明见解析;
(2)证明见解析;
(3)BD的长度为![]()
【解析】试题分析:(1)根据切线判定知道EB⊥BC,而AD⊥BC,从而可以确定AD∥BE,那么△BFC∽△DGC,又G是AD的中点,就可得出结论BF=EF.(2)要证PA是 O的切线,就是要证明∠PAO=90°连接AO,AB,根据第1的结论和BE是 O的切线和直角三角形的等量代换,就可得出结论.(3)点F作FH⊥AD于点H,根据前两问的结论,利用三角形的相似性和勾股定理,可以求出BD和FG的长度.
试题解析:(1)证明:连结![]() .
.
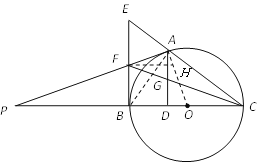
![]() 是⊙O的直径,
是⊙O的直径, ![]() .
.
在![]() 中,因为
中,因为![]() 是斜边
是斜边![]() 的中点,
的中点,
![]() .
. ![]() .
.
又![]() ,
, ![]() .
.
![]() 是⊙O的切线,
是⊙O的切线, ![]() .
.
![]() ,
,
![]() 是⊙O的切线.
是⊙O的切线.
(2)证明: ![]()
又![]() ,
, ![]() .
.
易证![]() ,
, ![]() .
.
![]()
![]() .
.
∵BF=EF
![]() .
.
(3)解:过点![]() 作
作![]() 于点
于点![]() .
.
![]() 四边形
四边形![]() 是矩形,
是矩形, ![]() .
.
由(1),∵BE=AF=FE.
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
∵四边形![]() 是矩形,
是矩形,
∴FH∥BC
![]()
![]()
∴![]() .
.
∵![]() ,
,
∴CF=3FG.
在Rt△FBC中,
∵CF=3FG,BF=FG,
∴CF2=BF2+BC2∴(3FG)2=FG2+(6![]() )2
)2
解得FG=3(负值舍去)
∴FG=3.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连结AC交EF于G,下列结论:①BE=DF;②∠AEF=15°;③AC垂直平分EF;④BE+DF=EF;⑤△CEF为等腰直角三角形,其中正确的有(填序号). 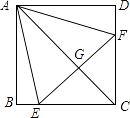
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个商场以同样的价格出售同样的商品,并且又各自推出不同的优惠措施,甲商场的优惠措施是:累计购买100元商品后,再买的商品按原价的90%收费;乙商场则是:累计购买50元商品后,再买商品按原价的95%收费,顾客选择哪个商店购物获得更多的优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将多项式﹣a2+a3+1﹣a按字母a升幂排列正确的是( )
A.a3﹣a2﹣a+1
B.﹣a﹣a2+a3+1
C.1+a3﹣a2﹣a
D.1﹣a﹣a2+a3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A、B、C,表示的数分别是﹣4、﹣2、3,请回答:
(1)若使C、B两点的距离与A、B两点的距离相等,则需将点C向左移动_____个单位;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,运动t秒钟过后:
①点A、B、C表示的数分别是_____、_____、_____ (用含t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2.试问:d1﹣d2的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求出d1﹣d2值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的材料,再回答后面的问题:
计算:10÷(![]() -
-![]() +
+![]() ).
).
解法一:原式=10÷![]() -10÷
-10÷![]() +10÷
+10÷![]() =10×2-10×3+10×6=50;
=10×2-10×3+10×6=50;
解法二:原式=10÷(![]() -
-![]() +
+![]() )=10÷
)=10÷![]() =10×3=30;
=10×3=30;
解法三:原式的倒数为(![]() -
-![]() +
+![]() )÷10
)÷10
=(![]() -
-![]() +
+![]() )×
)×![]() =
=![]() ×
×![]() -
-![]() ×
×![]() +
+![]() ×
×![]() =
=![]()
故原式=30.
(1)上面得到的结果不同,肯定有错误的解法,你认为解法 是错误的。
(2)请选择一种上述的正确方法解决下面的问题:
计算:(![]() )÷(
)÷(![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你从下列条件:①AB=CD,②AD=BC,③AB∥CD,④AD∥BC中任选两个,使它们能判定四边形ABCD是平行四边形.共有________种情况符合要求.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com