
【题目】如图,四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,将AC绕着点A顺时针旋转60°得AE,连接BE,CE.
(1)求证:△ADC≌△ABE;
(2)求证:![]()
(3)若AB=2,点Q在四边形ABCD内部运动,且满足![]() ,直接写出点Q运动路径的长度.
,直接写出点Q运动路径的长度.

【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)推出∠DAC=∠BAE,则可直接由SAS证明△ADC≌△ABE;
(2)证明△BCE是直角三角形,再证DC=BE,AC=CE即可推出结论;
(3)如图2,设Q为满足条件的点,将AQ绕着点A顺时针旋转60度得AF,连接QF,BF,QB,DQ,AF,证△ADQ≌△ABF,由勾股定理的逆定理证∠FBQ=90°,求出∠DQB=150°,确定点Q的路径为过B,D,C三点的圆上![]() ,求出
,求出![]() 的长即可.
的长即可.
(1)证明:∵∠CAE=∠DAB=60°,
∴∠CAE-∠CAB=∠DAB-∠CAB,
∴∠DAC=∠BAE,
又∵AD=AB,AC=AE,
∴△ADC≌△ABE(SAS);

(2)证明:在四边形ABCD中,
∠ADC+∠ABC=360°-∠DAB-∠DCB=270°,
∵△ADC≌△ABE,
∴∠ADC=∠ABE,CD=BE,
∴∠ABC+ABE=∠ABC+∠ADC=270°,
∴∠CBE=360°-(∠ABC+ABE)=90°,
∴CE2=BE2+BC2,
又∵AC=AE,∠CAE=60°,
∴△ACE是等边三角形,
∴CE=AC=AE,
∴AC2=DC2+BC2;
(3)解:如图2,设Q为满足条件的点,将AQ绕着点A顺时针旋转60度得AF,连接QF,BF,QB,DQ,AF,

则∠DAQ=∠BAF,AQ=QF,△AQF为等边三角形,
又∵AD=AB,
∴△ADQ≌△ABF(SAS),
∴AQ=FQ,BF=DQ,
∵AQ2=BQ2+DQ2,
∴FQ2=BQ2+BF2,
∴∠FBQ=90°,
∴∠AFB+∠AQB=360°-(∠QAF+∠FBQ)=210°,
∴∠AQD+∠AQB=210°,
∴∠DQB=360°-(∠AQD+∠AQB)=150°,
∴点Q的路径为过B,D,C三点的圆上![]() ,
,
如图2,设圆心为O,则∠BOD=2∠DCB=60°,
连接DB,则△ODB与△ADB为等边三角形,
∴DO=DB=AB=2,
∴点Q运动的路径长为:![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
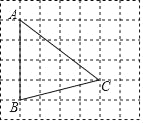
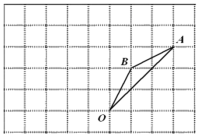
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长等于_____;
(Ⅱ)在线段AC上有一点D,满足AB2=ADAC,请在如图所示的网格中,用无刻度的直尺,画出点D,并简要说明点D的位置是如何找到的(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() .
.
(1)求证:无论k取什么实数值,这个方程总有实数根;
(2)当![]() =3时,△ABC的每条边长恰好都是方程
=3时,△ABC的每条边长恰好都是方程![]() 的根,求△ABC的周长.
的根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
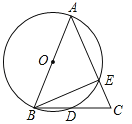
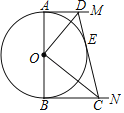
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧![]() 是劣弧
是劣弧![]() 的2倍;⑤AE=BC,其中正确的序号是_________.
的2倍;⑤AE=BC,其中正确的序号是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )

A.4:5B.2:5C.![]() :2D.
:2D.![]() :
:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要添置教师办公桌椅A、B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
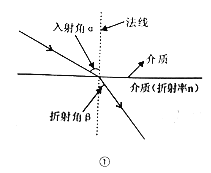
【题目】光线从空气射入水中会发生折射现象,发生折射时,满足的折射定律如图①所示:折射率![]() (
(![]() 代表入射角,
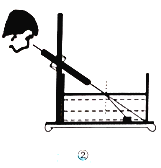
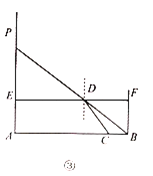
代表入射角,![]() 代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得
代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得![]() ,则光线从空射入水中的折射率n等于________.
,则光线从空射入水中的折射率n等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() ,
,![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,
,![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() .
.
(1)画出![]() ,直接写出点
,直接写出点![]() ,
,![]() 的坐标;
的坐标;
(2)求在旋转过程中,点![]() 经过的路径的长;
经过的路径的长;
(3)求在旋转过程中,线段![]() 所扫过的面积.
所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O直径AB=12cm,AM和BN是⊙O的切线,DC切⊙O于点E且交AM于点D,交BN于点C,设AD=x,BC=y.
(1)求y与x之间的关系式;
(2)x,y是关于t的一元二次方程2t2﹣30t+m=0的两个根,求x,y的值;
(3)在(2)的条件下,求△COD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com