
| A. | $\underbrace{55…5}_{2013个}$ | B. | $\underbrace{55…5}_{2014个}$ | C. | $\underbrace{55…5}_{2015个}$ | D. | $\underbrace{55…5}_{2016个}$ |
分析 当根式内的两个平方和的底数为1位数时,结果为5,当根式内的两个平方和的底数为2位数时,结果为55,当根式内的两个平方和的底数为3位数时,结果为555,当根式内的两个平方和的底数为2016位数时,结果为2016个5.
解答 解:∵$\sqrt{{4}^{2}+{3}^{2}}$=5,
$\sqrt{4{4}^{2}+3{3}^{2}}$=55
$\sqrt{44{4}^{2}+33{3}^{2}}$=555,
…,
∴$\sqrt{{{\underbrace{44…4}_{2016个}}^2}+{{\underbrace{33…3}_{2016个}}^2}}$=$\underset{\underbrace{55…5}}{2016个}$.
故选:D.
点评 此题主要考查了利用计算器进行数的开方,解题时先求出较简单的数,然后找出规律,推理出较大数的结果.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:选择题
 如图,用一个半径为30cm,面积为450πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
如图,用一个半径为30cm,面积为450πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )| A. | 5cm | B. | 10cm | C. | 15cm | D. | 5πcm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
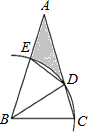 如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )
如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )| A. | 2$\sqrt{3}$+2-$\frac{5}{6}$π | B. | $\sqrt{3}$+1-$\frac{5}{3}$π | C. | 2$\sqrt{3}$+2-$\frac{1}{2}$π | D. | $\sqrt{3}$+1-$\frac{1}{2}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )
如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com