

分析 (1)根据各项百分比之和为1可得a的值;
(2)根据平均数、众数及中位数的定义求解可得;
(3)由条形图知1.70m的有2人,1.65m的有5人,共7人,据此可判断.
解答 解:(1)∵a%=1-(15%+30%+20%+10%)=25%,
∴a=25,
故答案为:25;
(2)平均数为$\frac{1.50×2+1.55×6+1.60×4+1.65×5+1.70×2}{2+6+4+5+2}$≈1.60(m),
1.55m出现次数最多,故众数为1.55m;
19个数据的中位数为第10个数据,故中位数为1.60m;
(3)由条形图知,分数从高到低1.70m的有2人,1.65m的有5人,共7人,
∴初赛成绩为1.60m的运动员不能进入复赛.
点评 本题考查了众数、平均数和中位数的定义及扇形统计图、条形统计图,根据扇形图和条形图得出解题所需数据及众数、平均数和中位数的定义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
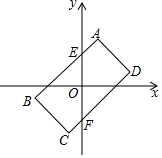 如图,四边形ABCD是以原点O为对称中心的矩形,A(1,3),D(3,1),AB和CD分别与y轴交于点E、F,连接OB.
如图,四边形ABCD是以原点O为对称中心的矩形,A(1,3),D(3,1),AB和CD分别与y轴交于点E、F,连接OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
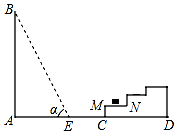 如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=34.5米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=20米,现有一只小猫睡在台阶的MN这层上晒太阳.($\sqrt{3}$取1.73)
如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=34.5米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=20米,现有一只小猫睡在台阶的MN这层上晒太阳.($\sqrt{3}$取1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com