
【题目】某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具.两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买![]() 个.如果甲、乙两商店分别购买玩具,两商店需付款总和为y元.
个.如果甲、乙两商店分别购买玩具,两商店需付款总和为y元.

(1)求y关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱;
(3)“六一”儿童节之后,该批发部对此玩具价格作了如下调整:数量不超过100个时,价格不变;数量超过100个时,每个玩具降价a元.在(2)的条件下,若甲、乙两商店“六一”儿童节之后去批发玩具,最多可节约2800元,求a的值.
【答案】(1)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时, ![]() ;(2)最多可节约9040-7200=1840元;(3)a=8.
;(2)最多可节约9040-7200=1840元;(3)a=8.
【解析】分析:
(1)设玩具的批发价为m,购买的数量为n,则由已知条件易得![]() (
(![]() );由题意可得
);由题意可得![]() ,由此可得
,由此可得![]() ,然后分①
,然后分①![]() ;②
;②![]() 两种情况结合已知条件求出y与x的函数关系式即可;
两种情况结合已知条件求出y与x的函数关系式即可;
(2)由题意将(1)中所得当![]() 时所得的函数关系式配方,即可求得两个商店分别购买所需资金的最大量,再由已知条件计算出两个商店联合购买所需的资金两,两者比较,即可得到所求的值;
时所得的函数关系式配方,即可求得两个商店分别购买所需资金的最大量,再由已知条件计算出两个商店联合购买所需的资金两,两者比较,即可得到所求的值;
(3)由题意可知,单独购买时,所需的最大金额不变,而联合购买所需资金为:120(60- a)=7200-120a,由题意可得:9040-(7200-120a)=2800,解此关于a的方程即可求得所求的值.
详解:
(1)由图可设玩具批发价m,数量为n,则m=kn+b(![]() ),
),
把 (50,80),(100,60)代入可求得![]() .
.
由题意得![]() ,解得
,解得![]() .
.
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时, ![]() .
.
(2)∵甲商店数量不超过100个,∴![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() .
.
∴x=70时,y最大值=9040(元).
两商店联合购买需120×60=7200(元),
∴最多可节约9040-7200=1840(元).
(3)单独购买不变,联合购买需120(60- a)=7200-120a(元),
∴9040-(7200-120a)=2800,解得a=8.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】寒假即将到来,外出旅游的人数逐渐增多,对旅行包的需求也将增多,某店准备到生产厂家购买旅行包,该厂有甲、乙两种新型旅行包.若购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元.
(1)甲、乙两种旅行包的进价分别是多少元?
(2)若该店恰好用了7000元购买旅行包;
①设该店购买了m个甲种旅行包,求该店购买乙种旅行包的个数;
②若该店将甲种旅行包的售价定为298元,乙种旅行包的售价定为325元,则当该店怎么样进货,才能获得最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
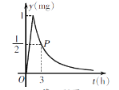
【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市移动通讯公司开设了两种通讯业务,A类是固定用户:先缴50元月租费,然后每通话1分钟再付话费0.4元;B类是“神州行”用户:使用者不缴月租费,每通话1分钟付话费0.6元(这里均指市内通话)。如果一个月内通话时间为x分钟,分别设A类和B类两种通讯方式的费用为y![]() 元和y
元和y![]() 元,
元,
(1)写出y![]() 、y
、y![]() 与x之间的函数关系式。
与x之间的函数关系式。
(2)一个月内通话多少分钟,用户选择A类合算?B类呢?
(3)若某人预计使用话费150元,他应选择哪种方式合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线PC交⊙O于A,C两点,AB是⊙O的直径,AD平分∠PAB交⊙O于点D,过D作DE垂直PA,垂足为E.
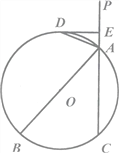
(1)求证:DE是⊙O的切线;
(2)若AE=1,AC=4,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,AC是⊙O的直径,D为⊙O上一点,过D作⊙O的切线交BA的延长线于P,且DP⊥BP于P.若PD+PA=6,AB=6,则⊙O的直径AC的长为( )
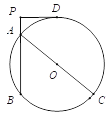
A. 5 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
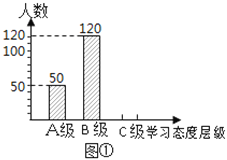
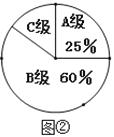
【题目】某市教育局对该市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了________名学生;
(2)图②中C级所占的圆心角的度数是__________;
(3)根据抽样调查结果,请你估计该市近20000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知A(0,a)、B(b, 0),且a、b满足: ![]() ,点D为x正半轴上一动点
,点D为x正半轴上一动点
(1)求A、B两点的坐标
(2)如图,∠ADO的平分线交y轴于点C,点 F为线段OD上一动点,过点F作CD的平行线交y轴于点H,且∠AFH=45°, 判断线段AH、FD、AD三者的数量关系,并予以证明
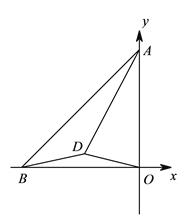
(3)以AO为腰,A为顶角顶点作等腰△ADO,若∠DBA=30°,直接写出∠DAO的度数

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com