
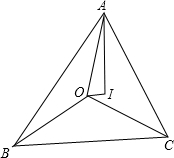
 在△ABC中,AB>AC,O、I分别是△ABC的外心和内心,且满足AB-AC=2OI,求证:
在△ABC中,AB>AC,O、I分别是△ABC的外心和内心,且满足AB-AC=2OI,求证:分析 (1)作IG⊥BC于G,IE⊥AC于E,IF⊥AB于F.,OD⊥BC于D,连接ID,则E、F、G是△ABC内切圆与各边的切点.首先证明OI=DG,再用同一法证明OI⊥IG即可解决问题.
(2)如图2中,连接BI、IC.由S△AOC=S△AIC+S△AOI+S△OIC,S△AOB=S△AIB-S△AOI-S△BOI,S△BOI=S△COI,推出S△AOC-S△AOB=S△AIC-S△AIB+2S△AOI+2S△BOI,求出
S△AIC-S△AIB以及2S△BOI,代入计算即可解决问题.
解答 证明:(1)作IG⊥BC于G,IE⊥AC于E,IF⊥AB于F.,OD⊥BC于D,连接ID,则E、F、G是△ABC内切圆与各边的切点.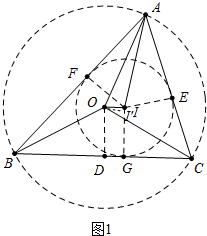
∵AB=AF+BF,AC=AE+CE,AF=AE,BF=BG,CE=CG,
∴AB-AC=BF-CE=BG-CG,
∵BG=BD+DG=$\frac{1}{2}$BC+DG,CG=CD-DG=$\frac{1}{2}$BC-DG,
∴AB-AC=($\frac{1}{2}$BC+DG)-($\frac{1}{2}$BC-DG)=2DG,
∵AB=AC=2OI,
∴DG=OI,
∵DG⊥IG,OD∥IG,作OI′⊥IG于I′,
∴OI′=DG=OI,
∴I与I′重合,
∴OI∥DG即OI∥BC.
(2)证明:如图2中,连接BI、IC.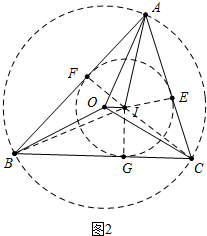
∵S△AOC=S△AIC+S△AOI+S△OIC,
S△AOB=S△AIB-S△AOI-S△BOI,S△BOI=S△COI,
∴S△AOC-S△AOB=S△AIC-S△AIB+2S△AOI+2S△BOI,
∵IF=IE=IG,AB-AC=2OI,
∴S△AIC-S△AIB=$\frac{1}{2}$AC•IE-$\frac{1}{2}$AB•IF=$\frac{1}{2}$(AC-AB)•IF=-OI•IF,
∵2S△BOI=2×$\frac{1}{2}$OI•IG=0I•IF,
∴S△AOC-S△AOB=-OI•IF+2S△AOI+OI•IF=2S△AOI.
点评 本题考查三角形外接圆、内切圆、切线长定理、平行线的性质和判定等知识,解题的关键是学会添加辅助线,灵活运用切线长定理解决问题,学会利用分割法求三角形的面积,题目比较难,属于计算类题目.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
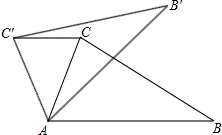 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com