

分析 设AD=k.根据图示找出线段间的数量关系:EF=AD-AE-FD;然后根据已知条件知AB=2AE,CD=2FD,EF=11cm;最后由这些关系式求得AD的值.
解答 解:设AD=k.
∵AB:BC:CD=3:2:4,
∴AB=$\frac{1}{3}$k,
∴AE=$\frac{1}{6}$k;CD=$\frac{4}{9}$k,FD=$\frac{2}{9}$k;
又∵EF=AD-AE-FD,EF=5.5cm,
∴k-$\frac{1}{6}$k-$\frac{2}{9}$k=11,
解得k=18(cm).
故AD的长为18cm.
点评 本题考查了两点间的距离以及中点的定义,解答此题时采用了数形结合的数学思想以及方程思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
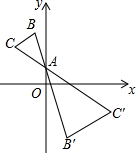 如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )
如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )| A. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n+3) | B. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n-3) | C. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n+2) | D. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
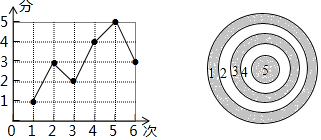 一种游戏如图,在一个定点位置用球拍扫动滑块,滑块落在圆环形靶图的相应位置,可以得到相应的分数.江小颖做6次的成绩如左图,对于这组数据,说法中不正确的是( )
一种游戏如图,在一个定点位置用球拍扫动滑块,滑块落在圆环形靶图的相应位置,可以得到相应的分数.江小颖做6次的成绩如左图,对于这组数据,说法中不正确的是( )| A. | 平均数3 | B. | 中位数3 | C. | 方差是2.5 | D. | 众数是3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a+1)2=2a2+1 | B. | (2a-1)2=4a2-1 | ||
| C. | (3a+2b)(3a-2b)=9a2-4b2 | D. | (2a-1)2=4a2+4a+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 完成下面推理过程.
完成下面推理过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com