
【题目】在平面直角坐标系中,已知二次函数![]() (a>0)图像与x轴交于点A、B(点A在点B的左侧),与y轴的交于点C,顶点为D .
(a>0)图像与x轴交于点A、B(点A在点B的左侧),与y轴的交于点C,顶点为D .
(1)求点A、B的坐标;
(2)若M为对称轴与x轴交点,且DM=2AM,
①求二次函数解析式;
②当30°<∠ADM<45°时,求a的取值范围.
【答案】(1)A(-1,0),B(3,0)(2)①![]() ②
②![]() <a<
<a<![]() .
.
【解析】
(1)根据自变量与函数值的对应关系,可得答案;
(2)①根据含数值相等点关于对称轴对称,可得抛物线的对称轴,根据DM与AM的关系,可得顶点的纵坐标,根据待定系数法,可得答案.
②根据正切函数,可得顶点的纵坐标,根据待定系数法,可得a的值,根据|a|的值越大,抛物线的开口越小,可得答案.
(1)令y=0,得![]() ,
,
解得![]() ,x2=3.
,x2=3.
∴A(-1,0),B(3,0).
(2)①∴AB=4.
∵抛物线对称轴为x=1,
∴AM=2.
∵DM=2AM,
∴DM=4.
∴D(1,-4).
∴a=1.
∴抛物线的表达式为![]()
②∴AB=4.
∵抛物线对称轴为x=1,
∴AM=2.
当∠ADM=45°时,tan45°=![]() =1,解得DM=2,
=1,解得DM=2,
即D(1,-2),
将D点坐标代入函数解析式,得
a-2a-3a=-2
a=![]() .
.
当∠ADM=30°时,tan30°=![]() =
=![]() ,解得DM=2
,解得DM=2![]() ,
,
即D(1,-2![]() ),
),
将D点坐标代入函数解析式,得
a-2a-3a=-2![]()
a=![]() .
.
由|a|的值越大,抛物线的开口越大小,得
30°<∠ADM<45°时,
∴![]() <a<
<a<![]() .
.


科目:初中数学 来源: 题型:
【题目】假定甲、乙两人在一次赛跑中,路程S与时间T的关系在平面直角坐标系中如图所示,请结合图形和数据回答问题:
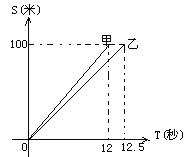
(1)这是一次 米赛跑;
(2)甲、乙两人中先到达终点的是 ;
(3)乙在这次赛跑中的速度为 ;
(4)甲到达终点时,乙离终点还有 米.
查看答案和解析>>
科目:初中数学 来源: 题型:
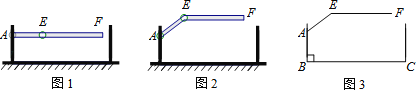
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条自南向北的大道上有O、A两个景点,O、A相距20km,在O处测得另一景点C位于点O的北偏东37°方向,在A处测得景点C位于点A的南偏东76°方向,且A、C相距13km .
(1)求:①A到OC之间的距离;
②O、C两景点之间的距离;
(2)若在O处测得景点B 位于景点O的正东方向10km,求B、C两景点之间的距离.(参考数据:tan37°=0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款30元的学生一共16人.
(1)孔明同学调查的这组学生共有_______人;
(2)这组数据的众数是_____元,中位数是_____元;
(3)若该校有2000名学生,都进行了捐款,估计全校学生共捐款多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
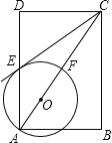
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD,AC分别交于点E,F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若AB=2,BC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P是⊙O外一点,PO交⊙O于点C,OC=CP=4,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com