

分析 (1)先证明四边形ACEF是平行四边形,再由矩形的性质证出AE⊥CF,即可得出四边形ACEF是菱形;
(2)由菱形的性质得出AC=CE,AD=ED,与三角函数得出CG=$\frac{3}{5}$CE=$\frac{3}{5}$AC,得出CG=3,CE=AC=5,由勾股定理求出EG=$\sqrt{C{E}^{2}-C{G}^{2}}$=4,在Rt△AEG中,由勾股定理求出AE=$\sqrt{A{G}^{2}+E{G}^{2}}$=4$\sqrt{5}$,即可得出AD的长.
解答 (1)证明:∵DE=AD,DF=CD.
∴四边形ACEF是平行四边形,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴AE⊥CF,
∴四边形ACEF是菱形;
(2)解:∵四边形ACEF是菱形,
∴AC=CE,AD=ED,
∵EG⊥AC,cos∠ECG=$\frac{CG}{CE}$=$\frac{3}{5}$,
∴CG=$\frac{3}{5}$CE=$\frac{3}{5}$AC,
∵AG=AC+CG=8,
∴CG=3,CE=AC=5,
∴EG=$\sqrt{C{E}^{2}-C{G}^{2}}$=4,
在Rt△AEG中,AE=$\sqrt{A{G}^{2}+E{G}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∴AD=$\frac{1}{2}$AE=2$\sqrt{5}$;
故答案为:2$\sqrt{5}$.
点评 本题考查了矩形的性质、菱形的判定与性质、平行四边形的判定、勾股定理、三角函数定义等知识;熟练掌握矩形的性质,证明四边形ACEF是菱形是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
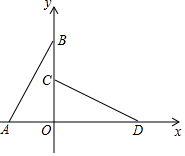 将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )
将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )| A. | $\frac{11π}{3}+2\sqrt{3}$ | B. | $3π+2\sqrt{3}$ | C. | $3π+\sqrt{3}$ | D. | $\frac{11π}{3}+\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:| 类别 | 频数 | 频率 |
| A | a | m |
| B | 35 | 0.35 |
| C | 20 | 0.20 |
| D | b | n |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com