
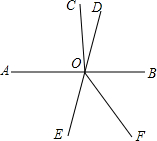
 如图,已知直线AB和ED相交于点O(∠AOE为锐角),射线OC⊥AB于点O,OF平分∠BOE.
如图,已知直线AB和ED相交于点O(∠AOE为锐角),射线OC⊥AB于点O,OF平分∠BOE.分析 (1)由垂直的定义得出∠COD+∠DOB=90°,根据邻补角定义可知∠DOB=180°-∠BOE,由角平分线定义得出∠BOE=2∠EOF,于是∠COD+180°-2∠EOF=90°,整理变形即可得出∠EOF-$\frac{1}{2}$∠COD=45°;
(2)首先求出∠DOF=∠DOB+∠BOF=135°-$\frac{1}{2}$∠COD.再由∠COD:∠DOF=4:25,得到∠COD:(135°-$\frac{1}{2}$∠COD)=4:25,求出∠COD=20°,那么∠BOD=70°,∠BOF=55°,∠AOD=110°,∠GOF=$\frac{2}{5}$∠AOD=44°,进而得出∠BOG=55°+44°=99°,或∠BOG=55°-44°=11°.
解答 (1)证明:∵射线OC⊥AB于点O,
∴∠COD+∠DOB=90°,
∵∠DOB=180°-∠BOE,∠BOE=2∠EOF,
∴∠COD+180°-2∠EOF=90°,
∴2∠EOF-∠COD=90°,
∴∠EOF-$\frac{1}{2}$∠COD=45°; (2)解:如图,∵∠EOF=45°+$\frac{1}{2}$∠COD,
(2)解:如图,∵∠EOF=45°+$\frac{1}{2}$∠COD,
∴∠EOB=90°+∠COD,
∠DOB=180°-∠EOB=90°-∠COD,
∠DOF=∠DOB+∠BOF=135°-$\frac{1}{2}$∠COD.
∵∠COD:∠DOF=4:25,
∴∠COD:(135°-$\frac{1}{2}$∠COD)=4:25,
∴∠COD=20°,
∴∠BOD=70°,∠BOF=55°,∠AOD=110°,∠GOF=$\frac{2}{5}$∠AOD=44°,
∴∠BOG=55°+44°=99°,或∠BOG=55°-44°=11°.
点评 本题考查了垂直的定义,对顶角、邻补角性质,角平分线定义,以及角度的计算,理解题意准确识图是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,三个全等的正方形内接于圆,正方形的边长为16,则圆的半径为( )
如图,三个全等的正方形内接于圆,正方形的边长为16,则圆的半径为( )| A. | $3\sqrt{33}$ | B. | $16\sqrt{5}$ | C. | $16\sqrt{2}$ | D. | $5\sqrt{17}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=3,y=2是方程3x-4y=1的一组解 | |
| B. | 方程3x-4y=1有无数组解,即x,y可以取任何数值 | |
| C. | 方程3x-4y=1只有两组解,两组解是:$\left\{\begin{array}{l}{x=1}\\{y=\frac{1}{2}}\end{array}\right.$和$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ | |
| D. | 方程3x-4y=1可能无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com