
�ڹ���202��·�Ľ�������,ij·�γ�4000��,�ɼ����������̶�����30���ڣ���30�죩�������.��֪�������̶Ӹ���10�����ˣ�������������̶ӵĹ���ȫ����������,���̶�ÿ��Ĺ�������ͬ,�ҹ��̶�ÿ��ÿ��Ĺ�������ͬ��.���̶�1�졢�ҹ���2�칲��·200�ף����̶�2�졢�ҹ��̶�3�칲��·350��.
(1)���ʼ����������̶�ÿ��ֱ���·������?
(2)�����������̶�ʩ��10���,���ڹ�����Ҫ��Ӽӳ��m��ȥѧϰ�¼���,�ܲ�Ҫ���ڹ涨ʱ�������,���ʼӿ��Գ��������?
(3)��֪���̶�ÿ���ʩ������Ϊ0.6��Ԫ,�ҹ��̶�ÿ���ʩ������Ϊ0.35��Ԫ,Ҫʹ�ù��̵�ʩ���������,�������Ӹ���������?��ͷ���Ϊ����?
��1�����̶�ÿ����·100�ף��ҹ��̶�ÿ����·50�ף�
(2)�ӿ��Գ��1�˻�2�ˣ�
(3)���̶�����30�죬�ҹ��̶�����20�죬��ͷ���Ϊ25��Ԫ��
���������������1�����ÿ����·x�ף��Ҷ�ÿ����·y�ף�Ȼ�����������·�ij��ȷֱ�Ϊ200��350������������ϵ�г������飬Ȼ��ⷽ���鼴�ɵý⣻
��2�����ݼӳ��m�˺���������·�ij��Ȳ�С��4000�ף��г�һԪһ�β���ʽ��Ȼ�����m��ȡֵ��Χ���ٸ���m�����������
��3������̶���a�죬�ҹ��̶���b�죬��������·�ij���Ϊ4000���г�������������a��ʾ��b���ٸ���0��b��30��ʾ��a��ȡֵ��Χ���ٸ����ܷ��õ������ӵķ���֮����ʽ������Ȼ�����һ�κ����������Խ��
�����������1�����ÿ����·x�ף��Ҷ�ÿ����·y�ף�
������ã� ��
��
��� ��
��
�𣺼��̶�ÿ����·100�ף��ҹ��̶�ÿ����·50�ף�
��2��������ã� ��
��
��ã� ��
��
��0��m��10��
�� ��
��
��m��������
��m=1��2��
��ӿ��Գ��1�˻�2�ˣ�
��3������̶���a�죬�ҹ��̶���b�죬
������ã�100a+50b=4000��
���ԣ�b=80��2a��
��0��b��30��
��0��80��2a��30��
���25��a��40��
�֡�0��a��30��
��25��a��30��
���ܷ���ΪWԪ��������ã�
W=0.6a+0.35b��
=0.6a+0.35��80��2a����
=��0.1a+28��
�ߩ�0.1��0��
�൱a=30ʱ��W��С=��0.1��30+28=25����Ԫ����
��ʱb=80��2a=80��2��30=20���죩��
�𣺼��̶�����30�죬�ҹ��̶�����20�죬��ͷ���Ϊ25��Ԫ��
���㣺1.��Ԫһ�η����飬2.����ʽ�飬3.һ�κ�����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��������֮һ��ˮ�ɻ�������ȫ��ij��ũҪ�������ͬ��800��ˮ�ɻ�����A��B��C�������ۣ�Ҫ������C�صļ���������A�ؼ�����3�������ص��˷����±���ʾ��
| | A�� | B�� | C�� |
| �˷ѣ�Ԫ/���� | 20 | 10 | 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij�̳�����һ�ֳɱ�Ϊÿ��60Ԫ�ķ�װ���涨�����ڼ����۵��۲����ڳɱ����ۣ��һ������ø���45%�����������֣�������y�����������۵���x��Ԫ������һ�κ���y=kx+b����x=65ʱ��y=55��x=75ʱ��y=45��
��1����һ�κ���y=kx+b�ı���ʽ��
��2�������̳��������ΪWԪ����д������W�����۵���x֮��Ĺ�ϵʽ�����۵��۶�Ϊ����Ԫʱ���̳��ɻ�����������������Ƕ���Ԫ��
��3�������̳����������500Ԫ����ȷ�����۵���x�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A����Ϊ��1��0������OAΪ���ڵ�һ���������ȱߡ�OAB��CΪx���������ϵ�һ�����㣨OC��1��������BC����BCΪ���ڵ�һ���������ȱߡ�BCD��ֱ��DA��y����E�㣮
��1����ͼ����C����x�����˶�ʱ����AC��x������x��ʾ�߶�AD�ij���
��2������C��ı仯��ֱ��AE��λ�ñ仯�����仯����˵�����ɣ������䣬�����ֱ��AE�Ľ���ʽ��
��3�����߶�BCΪֱ����Բ��Բ��Ϊ��F��
�ٵ�C���˶����δ�ʱֱ��EF��ֱ��BO����ʱ��F��ֱ��BO��λ�ù�ϵ��Σ���˵�����ɣ�
��GΪCD���F�Ľ��㣬HΪֱ��DF�ϵ�һ�����㣬����HG��HC����HG��HC����Сֵ����������Сֵ��x��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У�ֱ�� ��2��x�ᡢy��ֱ���A��B���㣬��ABΪ���ڵڶ���������������ABCD.
��2��x�ᡢy��ֱ���A��B���㣬��ABΪ���ڵڶ���������������ABCD.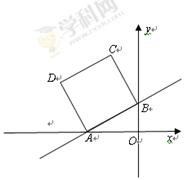
��1�����A��B�����꣬�����AB�ij���
��2�����D�͵�C�����ꣻ
��3�����ܷ���x������һ��M��ʹ��MDB���ܳ���С?����ܣ������M������ꣻ������ܣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
A��B����ͷ���150ǧ�ף��ʹ�˳����A���е�B���ҿʹ�������B��A�����ס������ʹ��ھ�ˮ�е��ٶ���ͬ��ͬʱ���������Ǻ��е�·��y��ǧ�ף��뺽��ʱ��x��ʱ���Ĺ�ϵ��ͼ��ʾ��
��1����ʹ��ھ�ˮ�е��ٶȼ�ˮ���ٶȣ�
��2��һ�һ�����A��ͷ˳�����е�B��ͷ�����ֱȿʹ���2Сʱ�����������ھ�ˮ�е��ٶ�Ϊ10ǧ��/ʱ���ڴ�����ϵ�л������ֺ���y��ǧ�ף���ʱ��x��ʱ���Ĺ�ϵͼ���������ʹ�������ʱ��A��ͷ��·�̡�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У�˫���� ��ֱ��y=kx+b����A��B���㣬��A������Ϊ����3��2����BC��y���ڵ�C����OC=6BC��
��ֱ��y=kx+b����A��B���㣬��A������Ϊ����3��2����BC��y���ڵ�C����OC=6BC��
��1����˫���ߺ�ֱ�ߵĽ���ʽ��
��2��ֱ��д������ʽ �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ƽ��ֱ������ϵxOy�У��� ��
�� �ֱ���
�ֱ��� �ᡢ
�ᡢ ����������ϣ���
����������ϣ��� ����
���� Ϊ�߶�
Ϊ�߶� ���е㣮
���е㣮
��1����ͼ1���߶� �ij���Ϊ________________��
�ij���Ϊ________________��
��2����ͼ2���� Ϊб��������ֱ��������
Ϊб��������ֱ�������� ������
������ �ڵ�һ����ʱ����ֱ��
�ڵ�һ����ʱ����ֱ�� ����Ӧ�ĺ����Ľ���ʽ��
����Ӧ�ĺ����Ľ���ʽ��
��3����ͼ3����� ��
�� �ֱ���
�ֱ��� �ᡢ
�ᡢ ��ĸ������ϣ���
��ĸ������ϣ��� ����
���� Ϊ���ڵ�����������������
Ϊ���ڵ����������������� ��������߶�
��������߶� ���ȵ����ֵ����ֱ��д����ʱֱ��
���ȵ����ֵ����ֱ��д����ʱֱ�� ����Ӧ�ĺ����Ľ���ʽ��
����Ӧ�ĺ����Ľ���ʽ��
|

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com