
如图,已知:四边形AEBD中,对角线AB和DE相交于点C,且AB垂直平分DE,AC=a,BC=b,CD=![]() ,其中a≥b>0.
,其中a≥b>0.
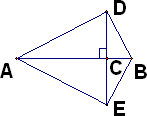
(1)用尺规作图法作出以AB为直径的⊙O;
(2)试判断点D与⊙O的位置关系,并说明理由;
(3)试估计代数式a+b和2![]() 的大小关系,并利用图形中线段的数量关系证明你的结论.
的大小关系,并利用图形中线段的数量关系证明你的结论.
|
解:(1)如图所示, 4分
注:必须保留作图痕迹,没有作图痕迹扣2分即作AB的垂直平分线不用圆规画,扣2分 (2)解法一:∵AC=a,BC=b,CD= ∴CD2=AC·CB,即 又∵∠DCA=∠DCB=90° ∴△DCA∽△BCD ∴∠DAB=∠CDB 7分 ∵∠DAB+∠ADC=90° ∴∠ADC+∠CDB=90°即∠ADB=90° ∴OA=OB=OD 9分 ∴点D在⊙O上 10分 解法二:在Rt△ACD中,AD2=AC2+CD2=a2+ab 在Rt△BCD中,BD2=BC2+CD2=b2+ab ∴AD2+BD2=a2+ab+b2+ab=a2+2ab+b2 6分 又∵AB2=(a+b)2=a2+2ab+b2 ∴AD2+BD2=AB2 8分 ∴△ABD是直角三角形,即∠ADB=90° ∴OA=OB=OD 9分 ∴点D在⊙O上 10分 (3)结论:a+b≥2 由(2)知,点D、E都在⊙O上 ∵AB是⊙O的直径,AB⊥DE ∴DE=2DC=2 ∵AB≥DE ∴a+b≥2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
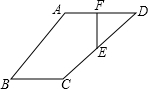 如图,已知在四边形ABCD中,E、F分别为AD、DC的中点,AD∥BC,AD:DC=1:
如图,已知在四边形ABCD中,E、F分别为AD、DC的中点,AD∥BC,AD:DC=1:| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
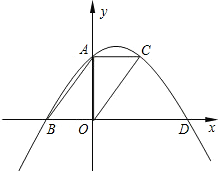 如图,已知平行四边形ABOC的顶点A、B、C在二次函数y=ax2+bx+c的图象上,又点A、B分别在y轴和x轴上,∠ABO=45°.图象顶点的横坐标为2,求二次函数解析式.
如图,已知平行四边形ABOC的顶点A、B、C在二次函数y=ax2+bx+c的图象上,又点A、B分别在y轴和x轴上,∠ABO=45°.图象顶点的横坐标为2,求二次函数解析式.查看答案和解析>>
科目:初中数学 来源: 题型:
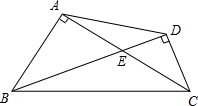 (2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25.
(2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com