
���� ��1����һ��һԪ���η���ʹ���ĸ�Ϊ1��2�����ݷ��̸��Ķ��壬������ô𰸣�
��2�����ڷ�����һ��������0��x��2������һ����Ϊ1�����ݸ���ϵ���Ĺ�ϵ�����-2+1=-1��-2��1=-2��Ȼ��д����-2��1Ϊ������һԪ���η���Ϊx2-x-2=0��
��3���������һԪ���η��̵ĸ��Ķ��塢һԪ���η��̵Ķ�����⣮
��� �⣺��1����һԪ���η���ʹ���ĸ�Ϊ1��2��
�ࣨx-1����x-2��=0��
�ʴ�Ϊ����x-1����x-2��=0��
��2����һ����Ϊ-2����һ����x����0��x��2������һ����Ϊ1��
��-2+1=-1��-2��1=-2��
����-2��1Ϊ������һԪ���η���Ϊx2-x-2=0��
�ʴ�Ϊ��x2-x-2=0��
��3���𰸲�Ψһ����һԪ���η���Ϊ2x2+bx+c=0��a��0������x=-3����ɵã�18-3b+c=0������ֻҪb��c��ֵ����3b-c=18���ɣ��磺b=0��c=-18ʱ��2x2-18=0��
�ʴ��ǣ�2x2-18=0��
���� ���⿼���˽�һԪ���η���--��ʽ�ֽⷨ�����̸������壮ע���������������ֱ�Ϊx1��x2����ɵ����з��������ķ���Ϊ����x-x1����x-x2��=0��


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪��A=60�㣬�����������ж�AB��CD���ǣ�������
��ͼ����֪��A=60�㣬�����������ж�AB��CD���ǣ�������| A�� | ��C=60�� | B�� | ��E=60�� | C�� | ��AFD=60�� | D�� | ��AFC=60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�����?ABCD���ڽǡ�BAD��ƽ���߽�BC�ڵ�E����AE=BE��
��ͼ�����?ABCD���ڽǡ�BAD��ƽ���߽�BC�ڵ�E����AE=BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪AB��CD��BEƽ�֡�ABC����CD��O�㣬��CDE=150�㣬���CΪ120�㣮
��ͼ����֪AB��CD��BEƽ�֡�ABC����CD��O�㣬��CDE=150�㣬���CΪ120�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=-2}\\{y=-3}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-x+4=0 | B�� | x=$\frac{1}{x}$ | C�� | x2-3x-2y=0 | D�� | x2+2=��x-1����x+2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
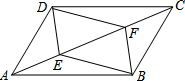 ��ƽ���ı���ABCD�У���E��F�ֱ��ڶԽ���AC�ϣ���AE=CF������DE��BE��DF��BF�����ı���DEBF��ƽ���ı�����Ϊʲô��
��ƽ���ı���ABCD�У���E��F�ֱ��ڶԽ���AC�ϣ���AE=CF������DE��BE��DF��BF�����ı���DEBF��ƽ���ı�����Ϊʲô���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com