
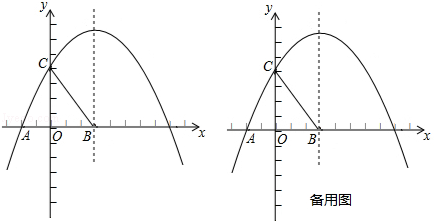
 x2+bx+c��ͼ��x����A��D���㣬������B�㣬��֪A�������ǣ�2��0����B��������ǣ�8��6����
x2+bx+c��ͼ��x����A��D���㣬������B�㣬��֪A�������ǣ�2��0����B��������ǣ�8��6���� S��BCD�������ڣ������P������ꣻ�������ڣ���˵�����ɣ�
S��BCD�������ڣ������P������ꣻ�������ڣ���˵�����ɣ�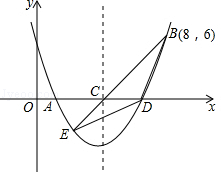
 x2��4x+6��
x2��4x+6��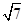 ��
��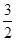 ����P2��4��
����P2��4��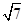 ��
��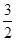 ����P3��3����
����P3��3����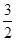 ����P4��5����
����P4��5����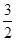 ����
���� S��BCD���h��ֵ������h��������ֵ�����P�ĺ����꼴�������P�����꣮
S��BCD���h��ֵ������h��������ֵ�����P�ĺ����꼴�������P�����꣮ x2+bx+c��ͼ���A��2��0����B��8��6��
x2+bx+c��ͼ���A��2��0����B��8��6��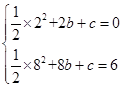 �����
�����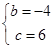
 x2��4x+6��
x2��4x+6�� x2��4x+6����y=
x2��4x+6����y= ��x��4��2��2��
��x��4��2��2�� x2+bx+c��x����������㣬
x2+bx+c��x����������㣬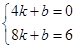 ���
���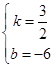
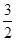 x��6��
x��6��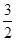 x��6��y=
x��6��y= x2��4x+6�Ľ��㣬
x2��4x+6�Ľ��㣬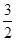 x��6=
x��6= x2��4x+6
x2��4x+6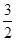 ����
���� ��2��6+
��2��6+ ��2��
��2��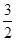 =7.5��
=7.5�� ��2��6=6��S��ADP=
��2��6=6��S��ADP= ��4��h=2h��
��4��h=2h�� S��BCD
S��BCD �����h=
�����h=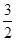 ��
��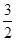 =
= x2��4x+6�����x1=4+
x2��4x+6�����x1=4+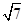 ��x2=4��
��x2=4��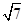 ��
��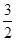 =
= x2��4x+6�����x1=3��x2=5��
x2��4x+6�����x1=3��x2=5��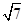 ��
��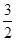 ����P2��4��
����P2��4��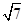 ��
��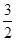 ����P3��3����
����P3��3����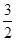 ����P4��5����
����P4��5����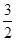 ����
����

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
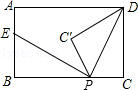
 �����㣬���E��x��y������������һ���㣬����x���·����ı���OEBF����OBΪ�Խ��ߵ�ƽ���ı��Σ�
�����㣬���E��x��y������������һ���㣬����x���·����ı���OEBF����OBΪ�Խ��ߵ�ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ���ҿյ��ɹ����۲�����1200Ԫ���ʸ��̼ҹ��м��ֽ���������
���ҿյ��ɹ����۲�����1200Ԫ���ʸ��̼ҹ��м��ֽ����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
A�� | B�� | C�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A����y=xֱ���� | B����ֱ��y=-x�� |
| C����x���� | D����y���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com