
 如图,二次函数的图象经过A(1,0),B(3,0)及在正比例函数y=x上的动点P
如图,二次函数的图象经过A(1,0),B(3,0)及在正比例函数y=x上的动点P| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 2 |
| 5 |
| 2 |
| 5 |
| 8 |
| 5 |
| 6 |
| 5 |


科目:初中数学 来源: 题型:
 有一块形状为平行四边形的铁片,用AB表示较长的一边,AD、BC表示较短的边,现有AB=2AD.现在想用这块铁片截一个直角三角形,并且希望以AB为斜边,直角顶点在CD上,问此想法是否可行?如果可行的话,请说明应该怎样截;如果不行,请说明理由.
有一块形状为平行四边形的铁片,用AB表示较长的一边,AD、BC表示较短的边,现有AB=2AD.现在想用这块铁片截一个直角三角形,并且希望以AB为斜边,直角顶点在CD上,问此想法是否可行?如果可行的话,请说明应该怎样截;如果不行,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知A(-4,0.5),B(-1,2)是一次函数y=ax+b与反比例函数y=
如图,已知A(-4,0.5),B(-1,2)是一次函数y=ax+b与反比例函数y=| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
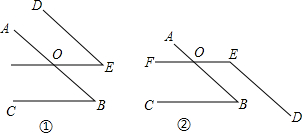
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,小明在河岸的A处观察对岸C处的一棵树,视线与河岸30°角;同时,小亮在距小明100米的河岸B观察对岸D处的一棵树,视线与河岸成75°角.已知河宽90米,且两岸平行,求河对岸C、D两棵树的距离.(参考数据:
如图,小明在河岸的A处观察对岸C处的一棵树,视线与河岸30°角;同时,小亮在距小明100米的河岸B观察对岸D处的一棵树,视线与河岸成75°角.已知河宽90米,且两岸平行,求河对岸C、D两棵树的距离.(参考数据:| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图为5×5的方格,其中有A、B、C三点,现有一点P在其它格点上,且A、B、C、P为轴对称图形,问共有几个这样的点P( )
如图为5×5的方格,其中有A、B、C三点,现有一点P在其它格点上,且A、B、C、P为轴对称图形,问共有几个这样的点P( )| A、5 | B、4 | C、3 | D、2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
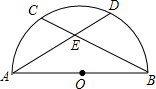 如图,已知:AB是⊙O的直径,C、D是弧
如图,已知:AB是⊙O的直径,C、D是弧 |
| AB |
| A、150° | B、135° |
| C、140° | D、120° |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com