
如图,在平面直角坐标系中直线y=x﹣2与y轴相交
于点A,与反比例函数在第一象限内的图象相交于点B(m,2)。
(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,
且△ABC的面积为18,求平移后的直线的函数关系式。
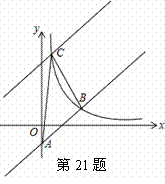
解:(1)将B坐标代入直线y=x﹣2中得:m﹣2=2,
解得:m=4,
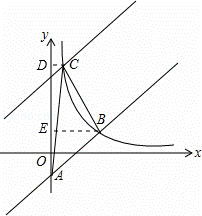 则B(4,2),即BE=4,OE=2,
则B(4,2),即BE=4,OE=2,
设反比例解析式为y=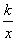 ,
,
将B(4,2)代入反比例解析式得:k=8,
则反比例解析式为y=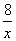 ;
;
(2)设平移后直线解析式为y=x+b,C(a,a+b),
对于直线y=x﹣2,令x=0求出y=﹣2,得到OA=2,
过C作CD⊥y轴,过B作BE⊥y轴,
将C坐标代入反比例解析式得:a(a+b)=8,
∵S△ABC=S梯形BCDE+S△ABE﹣S△ACD=18,
∴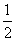 ×(a+4)×(a+b﹣2)+
×(a+4)×(a+b﹣2)+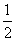 ×(2+2)×4﹣
×(2+2)×4﹣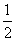 ×a×(a+b+2)=18,
×a×(a+b+2)=18,
解得:b=7,………1分
则平移后直线解析式为y=x+7。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
反比例函数y= 和正比例函数y=mx的部分图象如图所示.
和正比例函数y=mx的部分图象如图所示.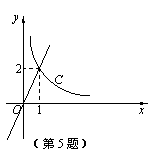 由此可以得到方程
由此可以得到方程 =mx的实数根为
=mx的实数根为
| A.x=1 | B.x=2 |
| C.x1=1,x2=-1 | D.x1=1,x2=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,两圆的圆心坐标分别为(-3,0)和(0,4),半径是方程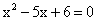 的两根,那么这两圆的位置关系是( )
的两根,那么这两圆的位置关系是( )
A、外离 B、相切 C、相交 D、内含
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系xoy中,菱形ABDC的边AB在x轴上,顶点C在y轴上,A(-6,0),C(0,8),抛物线y=ax2﹣10ax+c经过点C,且顶点M在直线BC上,则抛物线解析式为 ;若点P在抛物线上且满足S△PBD=S△PCD,则点P的坐标为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图下列四个几何体,它们各自的三视图(主视图、左视图、俯视图)中,有两个相同而另一个不同的几何体是( )
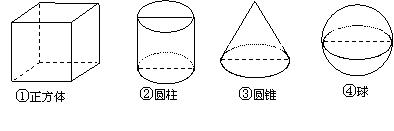 |
A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在⊿ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D。下列四个结论:
①以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切;
②∠BOC=90°+ ∠A;
∠A;
③EF不能成为⊿ABC的中位线;
④设OD=m,AE+AF=n,则S⊿AEF =mn.
其中正确的结论是:
A.①②③ B.①②④ C.②③④ D.①③④

查看答案和解析>>
科目:初中数学 来源: 题型:
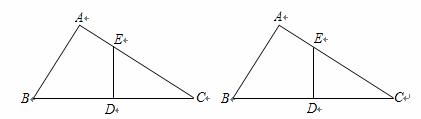
在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上一动点,点Q为边AC上一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)记线段PQ与线段DE的交点为点F,若△PDF为等腰三角形,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com