
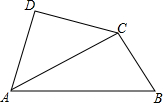
 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边AC与含45°角的三角尺(△ACD)的斜边AC恰好重合.已知AB=2$\sqrt{3}$,P是AC上的一个动点.
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边AC与含45°角的三角尺(△ACD)的斜边AC恰好重合.已知AB=2$\sqrt{3}$,P是AC上的一个动点.分析 (1)作DF⊥AC于F,由AB的长求得BC、AC的长.在等腰Rt△DAC中,DF=FA=FC;在Rt△BCP中,求得PC的长.则由勾股定理即可求得DP的长.
(2)由(1)得BC与DF的关系,则DP与DF的关系也已知,先求得∠PDF的度数,则∠PDA的度数也可求出,需注意有两种情况.
(3)由于四边形DPBQ为平行四边形,则BC∥DF,P为AC中点,作出平行四边形,求得面积.
解答 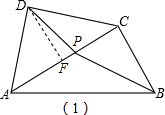 解:在Rt△ABC中,AB=2$\sqrt{3}$,∠BAC=30°,
解:在Rt△ABC中,AB=2$\sqrt{3}$,∠BAC=30°,
∴BC=$\sqrt{3}$,AC=3.
(1)如图(1),作DF⊥AC于F.
∵Rt△ACD中,AD=CD,
∴DF=AF=CF=$\frac{3}{2}$.
∵BP平分∠ABC,
∴∠PBC=30°,
∴CP=BC•tan30°=1,
∴PF=$\frac{1}{2}$,
∴DP=$\sqrt{D{F}^{2}+P{F}^{2}}$=$\frac{\sqrt{10}}{2}$.
(2)当P点位置如图(2)所示时,
根据(1)中结论,DF=$\frac{3}{2}$,∠ADF=45°,
又∵PD=BC=$\sqrt{3}$,
∴cos∠PDF=$\frac{DF}{PD}$=$\frac{\sqrt{3}}{2}$,
∴∠PDF=30°.
∴∠PDA=∠ADF-∠PDF=15°. 当P点位置如图(3)所示时,同(2)可得∠PDF=30°.
当P点位置如图(3)所示时,同(2)可得∠PDF=30°.
∴∠PDA=∠ADF+∠PDF=75°.
故∠PDA的度数为15°或75°;
(3)当点P运动到边AC中点(如图4),即CP=$\frac{3}{2}$时,
以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上.
∵四边形DPBQ为平行四边形,
∴BC∥DP,
∵∠ACB=90°,
∴∠DPC=90°,即DP⊥AC.
而在Rt△ABC中,AB=2$\sqrt{3}$,BC=$\sqrt{3}$,
∴根据勾股定理得:AC=3,
∵△DAC为等腰直角三角形,
∴DP=CP=$\frac{1}{2}$AC=$\frac{3}{2}$,
∵BC∥DP,
∴CP是平行四边形DPBQ的高,
∴S平行四边形DPBQ=DP•CP=$\frac{9}{4}$.
点评 本题考查了勾股定理,解直角三角形的应用,平行四边形的性质,综合性较强,难度系数较大,关键是熟练掌握好边角之间的关系.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com