
 如图所示,在平面直角坐标系xOy中,B1(1,0),B2(3,0),B3(6,0),B4(10,0),…,以B1B2为对角线作第一个正方形A1B1C1B2,以B2B3为对角线作第二个正方形A2B2C2B3,以B3B4为对角线作第三个正方形A3B3C3B4,…,如果所作正方形的对角线BnBn+1的长度依次增加1个单位长度,顶点An都在第一象限内(n≥1,且n为整数),用n的代数式表示An的横坐标为$\frac{(π+1)^{2}}{2}$.
如图所示,在平面直角坐标系xOy中,B1(1,0),B2(3,0),B3(6,0),B4(10,0),…,以B1B2为对角线作第一个正方形A1B1C1B2,以B2B3为对角线作第二个正方形A2B2C2B3,以B3B4为对角线作第三个正方形A3B3C3B4,…,如果所作正方形的对角线BnBn+1的长度依次增加1个单位长度,顶点An都在第一象限内(n≥1,且n为整数),用n的代数式表示An的横坐标为$\frac{(π+1)^{2}}{2}$. 分析 利用图形分别得出A点横坐标A1,A2,A3,…的横坐标分别为:$\frac{4}{2}$,$\frac{9}{2}$,$\frac{16}{2}$,$\frac{25}{2}$…,即可得出点A5的横坐标为:$\frac{36}{2}$,点An的横坐标为:$\frac{(n+1)^{2}}{2}$,再利用纵坐标变化规律进而得出答案.
解答 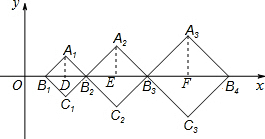 解:如图,分别过点A1,A2,A3,作A1D⊥x轴,A2E⊥x轴,A3F⊥x轴于点D,E,F,
解:如图,分别过点A1,A2,A3,作A1D⊥x轴,A2E⊥x轴,A3F⊥x轴于点D,E,F,
∵B1(1,0),
∴B1B2=3-1=2,B1D,=1,OD=2,B1D=A1D=1,
可得出A1(2,1),
∵B2(3,0),
∴B3B2=6-3=3,EA2=$\frac{3}{2}$,A2E=EB2=$\frac{3}{2}$,OE=6-$\frac{3}{2}$=$\frac{9}{2}$,
可得A2($\frac{9}{2}$,$\frac{3}{2}$),
同理可得出:A3(8,2),A4($\frac{25}{2}$,$\frac{5}{2}$),…,
∵A1,A2,A3,…的横坐标分别为:$\frac{4}{2}$,$\frac{9}{2}$,$\frac{16}{2}$,$\frac{25}{2}$…,
∴点An的横坐标为:$\frac{(n+1)^{2}}{2}$,
故答案为:$\frac{(n+1)^{2}}{2}$.
点评 此题主要考查了点的坐标规律,培养学生观察和归纳能力,从所给的数据和图形中寻求规律分别得出A点横纵坐标的规律是解答本题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
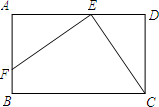 如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,则AE的长为6cm.
如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,则AE的长为6cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
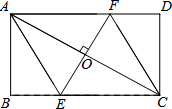 过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为( )
过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为( )| A. | 2 | B. | 3 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=-1.
如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com