
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љ ![]() x2+bx+cгыxжсНЛгкЕуAЃЌЕуBЃЌгыyжсНЛгкЕуCЃЌЕуBзјБъЮЊЃЈ6ЃЌ0ЃЉЃЌЕуCзјБъЮЊЃЈ0ЃЌ6ЃЉЃЌЕуDЪЧХзЮяЯпЕФЖЅЕуЃЌЙ§ЕуDзїxжсЕФДЙЯпЃЌДЙзуЮЊEЃЌСЌНгBDЃЎ
x2+bx+cгыxжсНЛгкЕуAЃЌЕуBЃЌгыyжсНЛгкЕуCЃЌЕуBзјБъЮЊЃЈ6ЃЌ0ЃЉЃЌЕуCзјБъЮЊЃЈ0ЃЌ6ЃЉЃЌЕуDЪЧХзЮяЯпЕФЖЅЕуЃЌЙ§ЕуDзїxжсЕФДЙЯпЃЌДЙзуЮЊEЃЌСЌНгBDЃЎ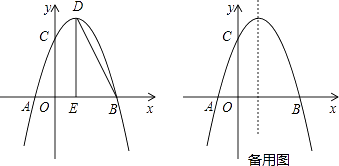
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЕуDЕФзјБъЃЛ
ЃЈ2ЃЉЕуFЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌЕБЁЯFBA=ЁЯBDEЪБЃЌЧѓЕуFЕФзјБъЃЛ
ЃЈ3ЃЉШєЕуMЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌЙ§ЕуMзїMNЁЮxжсгыХзЮяЯпНЛгкЕуNЃЌЕуPдкxжсЩЯЃЌЕуQдкЦНУцФкЃЌвдЯпЖЮMNЮЊЖдНЧЯпзїе§ЗНаЮMPNQЃЌЧыжБНгаДГіЕуQЕФзјБъЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКНЋЕуBЃЈ6ЃЌ0ЃЉЁЂCЃЈ0ЃЌ6ЃЉДњШыy=Љ ![]() x2+bx+cжаЃЌ
x2+bx+cжаЃЌ
ЕУЃК ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љ ![]() x2+2x+6ЃЎ
x2+2x+6ЃЎ
Ёпy=Љ ![]() x2+2x+6=Љ
x2+2x+6=Љ ![]() ЃЈxЉ2ЃЉ2+8ЃЌ
ЃЈxЉ2ЃЉ2+8ЃЌ
ЁрЕуDЕФзјБъЮЊЃЈ2ЃЌ8ЃЉЃЎ
ЃЈ2ЃЉ
НтЃКЩшЯпЖЮBFгыyжсНЛЕуЮЊЕуFЁфЃЌЩшЕуFЁфЕФзјБъЮЊЃЈ0ЃЌmЃЉЃЌШчЭМ1ЫљЪОЃЎ
ЁпЁЯFЁфBO=ЁЯFBA=ЁЯBDEЃЌЁЯFЁфOB=ЁЯBED=90ЁуЃЌ
ЁрЁїFЁфBOЁзЁїBDEЃЌ
Ёр ![]() ЃЎ
ЃЎ
ЁпЕуBЃЈ6ЃЌ0ЃЉЃЌЕуDЃЈ2ЃЌ8ЃЉЃЌ
ЁрЕуEЃЈ2ЃЌ0ЃЉЃЌBE=6Љ4=4ЃЌDE=8Љ0=8ЃЌOB=6ЃЌ
ЁрOFЁф= ![]() OB=3ЃЌ
OB=3ЃЌ
ЁрЕуFЁфЃЈ0ЃЌ3ЃЉЛђЃЈ0ЃЌЉ3ЃЉЃЎ
ЩшжБЯпBFЕФНтЮіЪНЮЊy=kxЁР3ЃЌ
дђга0=6k+3Лђ0=6kЉ3ЃЌ
НтЕУЃКk=Љ ![]() Лђk=
Лђk= ![]() ЃЌ
ЃЌ
ЁржБЯпBFЕФНтЮіЪНЮЊy=Љ ![]() x+3Лђy=
x+3Лђy= ![]() xЉ3ЃЎ
xЉ3ЃЎ
СЊСЂжБЯпBFгыХзЮяЯпЕФНтЮіЪНЕУЃК  ЂйЛђ
ЂйЛђ  ЂкЃЌ
ЂкЃЌ
НтЗНГЬзщЂйЕУЃК  Лђ
Лђ ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрЕуFЕФзјБъЮЊЃЈЉ1ЃЌ ![]() ЃЉЃЛ
ЃЉЃЛ
НтЗНГЬзщЂкЕУЃК  Лђ
Лђ ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрЕуFЕФзјБъЮЊЃЈЉ3ЃЌЉ ![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯПЩжЊЃКЕуFЕФзјБъЮЊЃЈЉ1ЃЌ ![]() ЃЉЛђЃЈЉ3ЃЌЉ
ЃЉЛђЃЈЉ3ЃЌЉ ![]() ЃЉ
ЃЉ

ЃЈ3ЃЉ
НтЃКЩшЖдНЧЯпMNЁЂPQНЛгкЕуOЁфЃЌШчЭМ2ЫљЪОЃЎ
ЁпЕуMЁЂNЙигкХзЮяЯпЖдГЦжсЖдГЦЃЌЧвЫФБпаЮMPNQЮЊе§ЗНаЮЃЌ
ЁрЕуPЮЊХзЮяЯпЖдГЦжсгыxжсЕФНЛЕуЃЌЕуQдкХзЮяЯпЖдГЦжсЩЯЃЌ
ЩшЕуQЕФзјБъЮЊЃЈ2ЃЌ2nЃЉЃЌдђЕуMЕФзјБъЮЊЃЈ2ЉnЃЌnЃЉЃЎ
ЁпЕуMдкХзЮяЯпy=Љ ![]() x2+2x+6ЕФЭМЯѓЩЯЃЌ
x2+2x+6ЕФЭМЯѓЩЯЃЌ
Ёрn=Љ ![]() +2ЃЈ2ЉnЃЉ+6ЃЌМДn2+2nЉ16=0ЃЌ
+2ЃЈ2ЉnЃЉ+6ЃЌМДn2+2nЉ16=0ЃЌ
НтЕУЃКn1= ![]() Љ1ЃЌn2=Љ
Љ1ЃЌn2=Љ ![]() Љ1ЃЎ
Љ1ЃЎ
ЁрЕуQЕФзјБъЮЊЃЈ2ЃЌ2 ![]() Љ2ЃЉЛђЃЈ2ЃЌЉ2
Љ2ЃЉЛђЃЈ2ЃЌЉ2 ![]() Љ2ЃЉЃЎ
Љ2ЃЉЃЎ

ЁОНтЮіЁПЃЈ1ЃЉгЩЕуBЁЂCЕФзјБъРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіХзЮяЯпЕФНтЮіЪНЃЌдйРћгУХфЗНЗЈНЋХзЮяЯпНтЮіЪНБфаЮГЩЖЅЕуЪНМДПЩЕУГіНсТлЃЛЃЈ2ЃЉЩшЯпЖЮBFгыyжсНЛЕуЮЊЕуFЁфЃЌЩшЕуFЁфЕФзјБъЮЊЃЈ0ЃЌmЃЉЃЌгЩЯрЫЦШ§НЧаЮЕФХаЖЈМАаджЪПЩЕУГіЕуFЁфЕФзјБъЃЌИљОнЕуBЁЂFЁфЕФзјБъРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіжБЯпBFЕФНтЮіЪНЃЌСЊСЂжБЯпBFКЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌНтЗНГЬзщМДПЩЧѓГіЕуFЕФзјБъЃЛЃЈ3ЃЉЩшЖдНЧЯпMNЁЂPQНЛгкЕуOЁфЃЌШчЭМ2ЫљЪОЃЎИљОнХзЮяЯпЕФЖдГЦадНсКЯе§ЗНаЮЕФаджЪПЩЕУГіЕуPЁЂQЕФЮЛжУЃЌЩшГіЕуQЕФзјБъЮЊЃЈ2ЃЌ2nЃЉЃЌгЩе§ЗНаЮЕФаджЪПЩЕУГіЕуMЕФзјБъЮЊЃЈ2ЉnЃЌnЃЉЃЎгЩЕуMдкХзЮяЯпЭМЯѓЩЯЃЌМДПЩЕУГіЙигкnЕФвЛдЊЖўДЮЗНГЬЃЌНтЗНГЬПЩЧѓГіnжЕЃЌДњШыЕуQЕФзјБъМДПЩЕУГіНсТлЃЎБОЬтПМВщСЫД§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§НтЮіЪНЁЂЯрЫЦШ§НЧаЮЕФХаЖЈМАаджЪЁЂе§ЗНаЮЕФаджЪМАНтвЛдЊЖўДЮЗНГЬЃЌНтЬтЕФЙиМќЪЧЃКЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіКЏЪ§НтЮіЪНЃЛЃЈ2ЃЉЧѓГіжБЯпBFЕФНтЮіЪНЃЛЃЈ3ЃЉЕУГіЙигкnЕФвЛдЊЖўДЮЗНГЬЃЎБОЬтЪєгкжаЕЕЬтЃЌФбЖШВЛДѓЃЌНтОіИУЬтаЭЬтФПЪБЃЌевГіЕуЕФзјБъРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіКЏЪ§НтЮіЪНЪЧЙиМќЃЎ
ЁОПМЕуОЋЮіЁПНтД№ДЫЬтЕФЙиМќдкгкРэНте§ЗНаЮЕФаджЪЕФЯрЙижЊЪЖЃЌеЦЮее§ЗНаЮЫФИіНЧЖМЪЧжБНЧЃЌЫФЬѕБпЖМЯрЕШЃЛе§ЗНаЮЕФСНЬѕЖдНЧЯпЯрЕШЃЌВЂЧвЛЅЯрДЙжБЦНЗжЃЌУПЬѕЖдНЧЯпЦНЗжвЛзщЖдНЧЃЛе§ЗНаЮЕФвЛЬѕЖдНЧЯпАбе§ЗНаЮЗжГЩСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЛе§ЗНаЮЕФЖдНЧЯпгыБпЕФМаНЧЪЧ45oЃЛе§ЗНаЮЕФСНЬѕЖдНЧЯпАбетИіе§ЗНаЮЗжГЩЫФИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЌвдМАЖдЯрЫЦШ§НЧаЮЕФаджЪЕФРэНтЃЌСЫНтЖдгІНЧЯрЕШЃЌЖдгІБпГЩБШР§ЕФСНИіШ§НЧаЮНазіЯрЫЦШ§НЧаЮЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
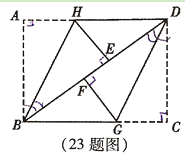
ЁОЬтФПЁП(10Зж) АбвЛеХОиаЮABCDжНЦЌАДШчЭМЗНЪНелЕўЃЌЪЙЕуAгыЕуEжиКЯЃЌЕуCгыЕуFжиКЯЃЈEЁЂFСНЕуОљдкBDЩЯЃЉЃЌелКлЗжБ№ЮЊBHЁЂDGЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїBHEЁеЁїDGFЃЛ
ЃЈ2ЃЉШєABЃН6cmЃЌBCЃН8cmЃЌЧѓЯпЖЮFGЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌAB=15ЃЌAC=13ЃЌBCБпЩЯИпAD=12ЃЌЪдЧѓЁїABCжмГЄЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬЈЗчЪЧвЛжжздШЛджКІЃЌЫќвдЬЈЗчжааФЮЊдВаФЃЌдкжмЮЇЪ§ЪЎЧЇУзЗЖЮЇФкаЮЦја§ЗчБЉЃЌгаМЋЧПЕФЦЦЛЕСІЃЌДЫЪБФГЬЈЗчжааФдкКЃгђBДІЃЌдкбиКЃГЧЪаAЕФе§ФЯЗНЯђ240ЧЇУзЃЌЦфжааФЗчСІЮЊ12МЖЃЌУПдЖРыЬЈЗчжааФ25ЧЇУзЃЌЬЈЗчОЭЛсМѕШѕвЛМЖЃЌШчЭМЫљЪОЃЌИУЬЈЗчжааФе§вд20ЧЇУз/ЪБЕФЫйЖШбиББЦЋЖЋ30ЁуЗНЯђЯђCвЦЖЏЃЌЧвЬЈЗчжааФЕФЗчСІВЛБфЃЌШєГЧЪаЫљЪмЗчСІДяЕНЛђГЌЙ§4МЖЃЌдђГЦЪмЬЈЗчгАЯьЃЎ ЪдЮЪЃК

ЃЈ1ЃЉAГЧЪаЪЧЗёЛсЪмЕНЬЈЗчгАЯьЃПЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШєЛсЪмЕНЬЈЗчгАЯьЃЌФЧУДЬЈЗчгАЯьИУГЧЪаЕФГжајЪБМфгаЖрГЄЃП
ЃЈ3ЃЉИУГЧЪаЪмЕНЬЈЗчгАЯьЕФзюДѓЗчСІЮЊМИМЖЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌвдABЮЊжБОЖЕФЁбOЗжБ№НЛЯпЖЮBCЃЌACгкЕуDЃЌEЃЌЙ§ЕуDзїDFЁЭACЃЌДЙзуЮЊFЃЌЯпЖЮFDЃЌABЕФбгГЄЯпЯрНЛгкЕуGЃЎ 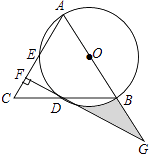
ЃЈ1ЃЉЧѓжЄЃКDFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєCF=1ЃЌDF= ![]() ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧЕШбќШ§НЧаЮЃЌ
ЪЧЕШбќШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
![]() ГпЙцзїЭМЃКзї
ГпЙцзїЭМЃКзї![]() ЕФНЧЦНЗжЯпBDЃЌНЛACгкЕу
ЕФНЧЦНЗжЯпBDЃЌНЛACгкЕу![]() БЃСєзїЭМКлМЃЃЌВЛаДзїЗЈ
БЃСєзїЭМКлМЃЃЌВЛаДзїЗЈ![]() ЃЛ
ЃЛ
![]() ХаЖЯ
ХаЖЯ![]() ЪЧЗёЮЊЕШбќШ§НЧаЮЃЌВЂЫЕУїРэгЩЃЎ
ЪЧЗёЮЊЕШбќШ§НЧаЮЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЫцЛњГщШЁВПЗжбЇЩњЃЌОЭЁАбЇЯАЯАЙпЁБНјааЕїВщЃЌНЋЁАЖдздМКзіДэЕФЬтФПНјааећРэЁЂЗжЮіЁЂИФе§ЁБЃЈбЁЯюЮЊЃККмЩйЁЂгаЪБЁЂГЃГЃЁЂзмЪЧЃЉЕФЕїВщЪ§ОнНјааСЫећРэЃЌЛцжЦГЩВПЗжЭГМЦЭМШчЯТЃК 
ЧыИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬт
ЃЈ1ЃЉИУЕїВщЕФбљБОШнСПЮЊ ЃЌ a=%ЃЌb=%ЃЌЁАГЃГЃЁБЖдгІЩШаЮЕФдВаФНЧЮЊЁу
ЃЈ2ЃЉЧыФуВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєИУаЃЙВга3200УћбЇЩњЃЌЧыФуЙРМЦЦфжаЁАзмЪЧЁБЖдДэЬтНјааећРэЁЂЗжЮіЁЂИФе§ЕФбЇЩњгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§НЧаЮABCжаЃЌЁЯACB=90ЁуЃЌЁЯB=50ЁуЃЌНЋДЫШ§НЧаЮШЦЕуCбиЫГЪБеыЗНЯђа§зЊКѓЕУЕНШ§НЧаЮAЁфBЁфCЃЌШєЕуBЁфЧЁКУТфдкЯпЖЮABЩЯЃЌACЁЂAЁфBЁфНЛгкЕуOЃЌдђЁЯCOAЁфЕФЖШЪ§ЪЧЃЈ ЃЉ 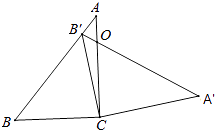
A.50Ёу
B.60Ёу
C.70Ёу
D.80Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЮвЙњМИМввјааЕФБъжОЃЌЦфжаМДЪЧжсЖдГЦЭМаЮгжЪЧжааФЖдГЦЭМаЮЕФгаЃЈ ЃЉ 
A.2Иі
B.3Иі
C.4Иі
D.5Иі
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com