
【题目】数学实践小组想利用镜子的反射测量池塘边一棵树的高度AB.测量和计算的部分步骤如下:

①如图,树与地面垂直,在地面上的点C处放置一块镜子,小明站在BC的延长线上,当小明在镜子中刚好看到树的顶点A时,测得小明到镜子的距离CD=2米,小明的眼睛E到地面的距离ED=1.5米;
②将镜子从点C沿BC的延长线向后移动10米到点F处,小明向后移动到点H处时,小明的眼睛G又刚好在镜子中看到树的顶点A,这时测得小明到镜子的距离FH=3米;
③计算树的高度AB;
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°(AC>BC),用尺规作图的方法作线段AD,保留作图痕迹如图所示,认真观察作图痕迹,若CD=4,BD=5,则AC的长为( )
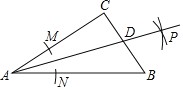
A.6B.9C.12D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与函数
,与函数![]() 的图象的一个交点为
的图象的一个交点为![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)将线段![]() 向右平移得到对应线段
向右平移得到对应线段![]() ,当点
,当点![]() 落在函数
落在函数![]() 的图象上时,求线段
的图象上时,求线段![]() 扫过的面积.
扫过的面积.
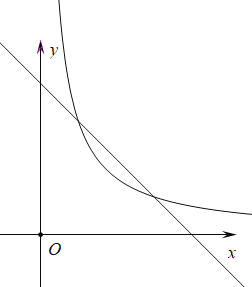
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交点
轴交点![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .如图1,点
.如图1,点![]() 为抛物线上任意一点,过点
为抛物线上任意一点,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() .
.
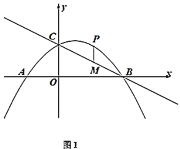
(1)求抛物线的解析式;
(2)当![]() 是直角三角形时,求
是直角三角形时,求![]() 点坐标;
点坐标;
(3)如图2,作![]() 点关于直线
点关于直线![]() 的对称点
的对称点![]() ,作直线
,作直线![]() 与抛物线交于
与抛物线交于![]() ,设抛物线对称轴与
,设抛物线对称轴与![]() 轴交点为
轴交点为![]() ,当直线
,当直线![]() 经过点
经过点![]() 时,请你直接写出
时,请你直接写出![]() 的长.
的长.
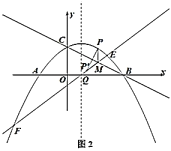
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O的直径,点C,D在⊙O上,![]() 连接AD,OC.
连接AD,OC.
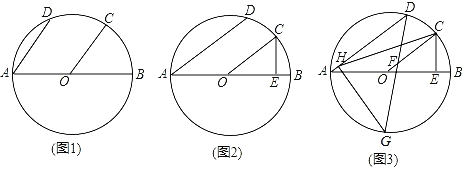
(1)如图1,求证:AD∥OC;
(2)如图2,过点C作CE⊥AB于点E,求证:AD=2OE;
(3)如图3,在(2)的条件下,点F在OC上,且OF=BE,连接DF并延长交⊙O于点G,过点G作CH⊥AD于点H,连接CH,若∠CFG=135°,CE=3,求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
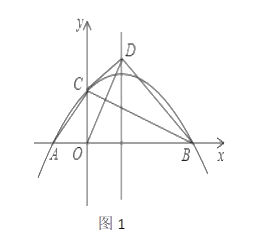
【题目】如图,在平面直角坐标系中,抛物线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 将
将![]() 沿
沿![]() 所在的直线翻折,得到
所在的直线翻折,得到![]() 连接
连接![]() .
.
(1)若![]() 求抛物线的解析式.
求抛物线的解析式.
(2)如图1,设![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,![]() 若
若![]() 点是半径为
点是半径为![]() 的
的![]() 上一动点,连接
上一动点,连接![]() 当点
当点![]() 运动到某一位置时,
运动到某一位置时,![]() 的值最大,请求出这个最大值,并说明理由.
的值最大,请求出这个最大值,并说明理由.
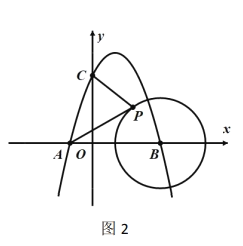
查看答案和解析>>
科目:初中数学 来源: 题型:
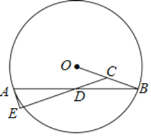
【题目】如图,在⊙O中,C,D分别为半径OB,弦AB的中点,连接CD并延长,交过点A的切线于点E.
(1)求证:AE⊥CE.
(2)若AE=2,sin∠ADE=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com