
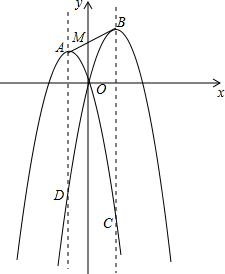
 如图,抛物线C1:y=-(x+m)2+m2(m>0)的顶点为A,抛物线C2:y=-(x-n)2+n2(n>m)的顶点为B,抛物线C2的对称轴与抛物线C1相交于点C,抛物线C1的对称轴与抛物线C2相交于点D.
如图,抛物线C1:y=-(x+m)2+m2(m>0)的顶点为A,抛物线C2:y=-(x-n)2+n2(n>m)的顶点为B,抛物线C2的对称轴与抛物线C1相交于点C,抛物线C1的对称轴与抛物线C2相交于点D.分析 (1)AD用A与D的纵坐标之差表示,BC用B与C的纵坐标之差表示;
(2)先求AB的解析式,再确定B点坐标,再用两点间的距离公式求出AM与BM;
(3)如果△AND∽△BMC,那么必有∠NAD=∠MBC,由于AD∥BC,故延长BA与抛物线的交点就是N,利用两边对应成比例列出线段等式,然后对等式进行恒等变形即可得出结论.当然,各线段要用m与n表示.
解答 解:(1)由顶点坐标,得
A(-m,m2);B(n,n2).
直线AD:x=-m,直线BC:x=n.
把x=-m代入C2:y=-(x-n)2+n2,y=-m2-2mn,即D(-m,-m2-2mn);
把x=n代入C1:Y=-(x+m)2+m2,解得y=-n2-2mn,即C(n,-n2-2mn).
AD=m2-(-m2-2mn)=2m2+2mn,
BC=n2-(-n2-2mn)=2n2+2mn;
(2)由C1是y=-(x+1)2+1,OM=3,得A(-1,1),M(0,3).
设AM的解析式为y=kx+b,将A,B点坐标代入,得
$\left\{\begin{array}{l}{-k+b=1}\\{b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=3}\end{array}\right.$.
故直线AB的解析式为y=2x+3,
把B(n,n2)代入y=2x+3得
n=-1(舍),n=3,
n2=9,B(3,9)
C2:y=-(x-3)2+9;
$\frac{AM}{BM}$=$\frac{\sqrt{1+(3-1)^{2}}}{\sqrt{{3}^{2}+(9-3)^{2}}}$=$\frac{\sqrt{5}}{\sqrt{45}}$=$\frac{1}{3}$;
(3)∵△AND∽△BMC,∴∠NAD=∠MBC,
∵AD∥BC,
故延长BA与抛物线的交点就是N,如图,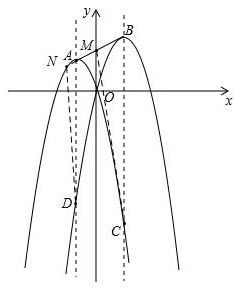
由A(-m,m2)、B(n,n2)求得直线AB的解析式为:y=(n-m)x+mn,
则$\left\{\begin{array}{l}{y=(n-m)x+mn}\\{y=-(x+m)^{2}+{m}^{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-n}\\{y=-{n}^{2}+2mn}\end{array}\right.$或$\left\{\begin{array}{l}{x=-m}\\{y={m}^{2}}\end{array}\right.$(舍去),
∴N(-n,-n2+2mn),
∴AN2=(-n+m)2+(-n2+2mn-m2)2=(n-m)2[1+(n-m)2],
BM2=n2+(n2-mn)2=n2[1+(n-m)2],
AD2=(2m2+2mn)2=4m2(m+n)2,
BC2=(2n2+2mn)2=4n2(m+n)2,
∵$\frac{A{N}^{2}}{B{M}^{2}}=\frac{A{D}^{2}}{B{C}^{2}}$,
∴$\frac{{(n-m)}^{2}[1+{(n-m)}^{2}]}{{n}^{2}[1+{(n-m)}^{2}]}$=$\frac{4{m}^{2}{(m+n)}^{2}}{4{n}^{2}{(m+n)}^{2}}$,
∴$\frac{n-m}{n}=\frac{m}{n}$,
∴n=2m.
根据抛物线的对称性可知,N(-n,-n2+2mn)关于对称轴AD的对称点为N'(-2m+n,-n2+2mn)也是符合要求的点,由于AN2=(-n+m)2+(-n2+2mn-m2)2=(n-m)2[1+(n-m)2]=AN'2=(-n+m)2+(-n2+2mn-m2)2=(n-m)2[1+(n-m)2],所以结果同上,不受影响.
综上所述,n=2m.
点评 本题考查了待定系数法求二次函数与一次函数解析式、相似三角形的判定与性质、平行线的性质、两点间的距离公式、解二元二次方程组等知识点,难度较大.本题多次用到两点间的距离公式,熟练掌握公式是关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
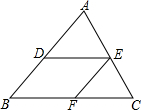 如图,DE∥BC,EF∥AB,则:
如图,DE∥BC,EF∥AB,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com