
分析 (1)由等式左边两数的底数可知,两底数是相邻的两个自然数,右边为两底数的和,由此得出规律;
(2)等式左边减数的底数与序号相同,由此得出第n个式子,根据整式的运算展开、合并即可验证;
(3)由3=22-12,5=32-22,7=42-32,…,将算式逐一变形,再寻找抵消规律.
解答 解:(1)依题意,得第⑥个算式为:72-62=13;
故答案为:72-62=13;
(2)根据几个等式的规律可知,第n个式子为:(n+1)2-n2=2n+1;
∵左边=n2+2n+1-n2=2n+1=右边,
∴(n+1)2-n2=2n+1;
(3)由(2)的规律可知,
1+3+5+7+…+99
=1+(22-12)+(32-22)+(42-32)+…+(512-502)
=512
=2061.
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律,利用规律解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
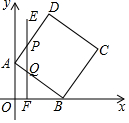 如图,点A(0,3),B(4,0),以AB为边作正方形ABCD,点F是射线OB上一动点,过点F作EF⊥x轴交正方形ABCD于P,Q两点,设OF=x,△APQ的面积为y,下列图象中,能表示y与x之间的函数关系的图象大致是( )
如图,点A(0,3),B(4,0),以AB为边作正方形ABCD,点F是射线OB上一动点,过点F作EF⊥x轴交正方形ABCD于P,Q两点,设OF=x,△APQ的面积为y,下列图象中,能表示y与x之间的函数关系的图象大致是( )| A. | 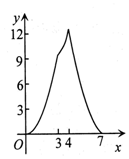 | B. | 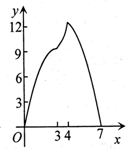 | C. | 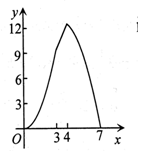 | D. | 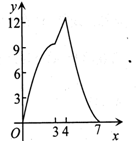 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
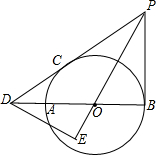 如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E.
如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com