

分析 (1)根据与x轴有唯一交点,即△=0,即可求出a的值;
(2)用含a的式子表示出各点的坐标,根据待定系数法求出直线BC解析式,根据AE∥BC,求出直线AE的解析式,根据直线与抛物线相交,即可求出点E的横坐标,即可证明;
(3)根据题意,求出抛物线C2的解析式,即可得到|OM|=|0N|,根据面积的关系,得到点P,点Q的横坐标之间的关系,再抛物线与直线相交,得到一元二次方程,利用根与系数的关系即可求得k值.
解答 (1)解:根据C1与x轴有唯一交点,可得:△=b2-4ac=16-16a2=0,
解得:a=1,或a=-1(不合题意,舍去),
∴C1的解析式为:y=x2+4x+4.
(2)证明:∵A(1,y1),B(0,y2),C(-1,y3)三点均在C1上,
∴A(1,5a+4),B(0,4a),C(-1,5a-4),且0<a<2,
设直线BC的解析式为:y=kx+b,点B、C在直线BC上,得:$\left\{\begin{array}{l}{b=4a}\\{-k+b=3a-4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=4-a}\\{b=4a}\end{array}\right.$,
∴直线BC的解析式为:y=(4-a)x+4a,
由AE∥BC,可得直线AE的解析式为:y=(4-a)x+6a,
AE交抛物线C1于E,可得:ax2+4x+4a=(4-a)x+6a,解得:x=-2或x=1(舍去),
∴点E在直线x=1的直线上.
(3)解:当a=1时,抛物线解析式为:y=x2+4x+4,
将抛物线C1先向右平移2个单位,再向下平移1个单位得抛物线C2的解析式为:y=x2-1,
∴可得点M(-1,0),N(1,0),
∴|OM|=|0N|,
设点P(x1,kx1),Q(x2,kx2),(x1<0,x2>0,k>0),
由△NOQ的面积是△MOP的面积的4倍,可知:kx2=4(-kx1),
即 x2=-4x1,
由y=kx且y=x2-1,可得:x2-kx-1=0,
∴x1+x2=k,且x1•x2=-1,且 x2=-4x1,
解得:${x}_{1}=-\frac{1}{2}$,x2=2,$k=\frac{3}{2}$.
点评 本题主要考查二次函数与一次函数的综合应用,在第(3)小题中,能根据三角形的面积之间的关系,找到点P,点Q的横坐标之间的关系是解答此题的关键.


科目:初中数学 来源: 题型:填空题
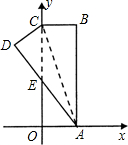 如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.若双曲线$y=\frac{k}{x}$经过点D,则k=-$\frac{48}{25}$.
如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.若双曲线$y=\frac{k}{x}$经过点D,则k=-$\frac{48}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.4×103元 | B. | 1.4×1011元 | C. | 14×1010元 | D. | 0.14×1012元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com