
 ��ͼ��������y=-x2+bx+c��x��ĸ������ཻ�ڵ�A��-1��0������y���ཻ�ڵ�B��0��3����
��ͼ��������y=-x2+bx+c��x��ĸ������ཻ�ڵ�A��-1��0������y���ཻ�ڵ�B��0��3�������� ��1���ô���ϵ����ֱ����������߽���ʽ��
��2�������P�����꣬��ʾ��AB2=102��PB2=1+��t-3��2��PA2=4+t2���������������������⼴�ɣ�
��3�������������ABD������������ó�������MAB������������MN�Ľ���ʽ��������������⼴�ɣ�
��4������DE��FG��Ҫʹ��D��E��F��GΪ������ı���Ϊƽ���ı��Σ�ֻ��DE=FG����t��0����������⼴�ɺ�t��0�жϲ���������������ƽ�ƺ��ֱ�ߣ�
��� �⣺��1����������y=-x2+bx+c��x��ĸ������ཻ�ڵ�A��-1��0������y���ཻ�ڵ�B��0��3����
��$\left\{\begin{array}{l}{-1-b+c=0}\\{c=3}\end{array}\right.$��
��$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$��
�������ߵĽ���ʽΪy=-x2+2x+3��
��������D��1��4����
��2�����P��1��t����
��A��-1��0����B��0��3��
��AB2=102��PB2=1+��t-3��2��PA2=4+t2��
�ٵ�PA=PBʱ������1+��t-3��2=4+t2��
��t=1��
��P1��1��1����
�ڵ�AB=APʱ������4+t2=10��
��t=��$\sqrt{6}$��\
��P2��1��$\sqrt{6}$����P3��1��-$\sqrt{6}$����
�۵�BP=BAʱ������1+��t-3��2=10��
��t=0����t=6���ᣩ
��P4��1��0����
��P1��1��1����P2��1��$\sqrt{6}$����P3��1��-$\sqrt{6}$����P4��1��0����
��3�����ڣ�
��ͼ��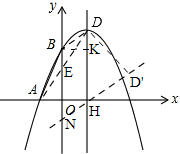
��D��1��4����A��-1��0����
��ֱ��AD����ʽΪy=2x+2��
��E��0��2����
��B��0��3����
��BE=1��
��S��ABD=S��ABE+S��DBE=$\frac{1}{2}$BE��|xA|+$\frac{1}{2}$BE��|xD|=$\frac{1}{2}$BE��|xA|+|xD|��=$\frac{1}{2}$��1����1+1��=1
��B��0��3����D��1��4����
��BD=$\sqrt{2}$��
ֱ��BD����ʽΪy=x+3��
��S��MBD=2S��ABD=2��
���M��ֱ��BD �ľ���Ϊ2$\sqrt{2}$��
��M��ֱ��MN��BD�����Գ����ڵ�H������D��DD'��MN������B��BK��DH��
���DD'H�ס�BKD��
��$\frac{DH}{BD}=\frac{DD'}{BK}$��
��H��1��0����
ֱ��MN�Ľ���ʽΪy=x-1�٣�
�������ߵĽ���ʽΪy=-x2+2x+3�ڣ�
�����٢����x=$\frac{1+\sqrt{17}}{2}$��x=$\frac{1-\sqrt{17}}{2}$��
��M1��$\frac{1+\sqrt{17}}{2}$��$\frac{\sqrt{17}-1}{2}$����M2��$\frac{1-\sqrt{17}}{2}$��$\frac{-\sqrt{17}-1}{2}$����
��4����ͼ1��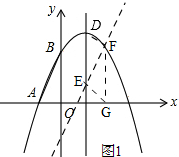
��A��-1��0����B��0��3����
��ֱ��AB����ʽΪy=3x+3��
��E��1��t����
��ֱ��EF����ʽΪy=3x+t-3��
��D��1��4����
��DE=|4-t|
�ٵ�t��0ʱ��
����D��E��F��GΪ������ı���Ϊƽ���ı��Σ���DE��FG��
��DE=FG=4-t��
����F��������Ϊ4-t��
��F��ֱ��EF�ϣ�
��F��$\frac{7-2t}{3}$��4-t����
��F��������y=-x2+2x+3�ϣ�
��t=$\frac{25-3\sqrt{41}}{8}$��t=$\frac{25+3\sqrt{41}}{8}$��
��ƽ�ƺ�ֱ��AB�Ľ���ʽΪy=3x+$\frac{1-3\sqrt{41}}{8}$��y=3x+$\frac{1+3\sqrt{41}}{8}$���ᣩ
�ڵ�t��0ʱ��OE��FG
��DE��FG��
������D��E��F��GΪ������ı��β�����Ϊƽ���ı��Σ�
����������ƽ�ƺ�ֱ��AB�Ľ���ʽΪy=3x+$\frac{1-3\sqrt{41}}{8}$��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ���������������ε����ʣ������ε�������㵽ֱ�ߵľ��룬ƽ���ı��ε����ʣ��Ȿ��Ĺؼ������ֱ��MN�Ľ���ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=-x+2��ͼ��ֱ�x��y���ڵ�A��B����һֱ��y=kx+b��k��0��������C��1��0���Ұѡ�AOB������ֳ������֣�
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=-x+2��ͼ��ֱ�x��y���ڵ�A��B����һֱ��y=kx+b��k��0��������C��1��0���Ұѡ�AOB������ֳ������֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
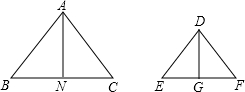 ��֪���ڡ�ABC���DEF�У�AN��BC��N��DG��EF��G��$\frac{AB}{DG}$=$\frac{AC}{DF}$=$\frac{AN}{DG}$����֤����ABC�ס�DEF��
��֪���ڡ�ABC���DEF�У�AN��BC��N��DG��EF��G��$\frac{AB}{DG}$=$\frac{AC}{DF}$=$\frac{AN}{DG}$����֤����ABC�ס�DEF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��C�������CE��ֱ����AD�ڵ�E����OD��AC�ڵ�F��
��ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��C�������CE��ֱ����AD�ڵ�E����OD��AC�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com