
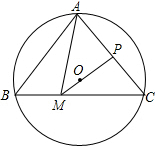
 如图,△ABC内接于⊙O,若∠BAC=80°,∠C=50°,取AC中点P,连接PO并延长交BC于点M,连接AM,则∠BAM=( )
如图,△ABC内接于⊙O,若∠BAC=80°,∠C=50°,取AC中点P,连接PO并延长交BC于点M,连接AM,则∠BAM=( )| A. | 45° | B. | 30° | C. | 50° | D. | 55° |
分析 根据垂径定理,由题意可得,OP垂直平分AC,由∠BAC=80°,∠C=50°,可以得到∠B的度数,从而可以求得∠BAM的度数.
解答 解:∵∠BAC=80°,∠C=50°,
∴∠B=180°-80°-50°=50°,
∵点P为AC的中点,点O为⊙O的圆心,
∴MP⊥AC,
∴MA=MC,∠MPC=∠MPA=90°,∠AMP=∠CMP,
∴∠CMP=∠MPC-∠C=40°,
∴∠AMC=80°,
又∵∠B=50°,∠AMC=∠B+∠BAM,
∴∠BAM=80°-50°=30°,
故选B.
点评 本题考查垂径定理、圆周角定理,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


科目:初中数学 来源: 题型:解答题
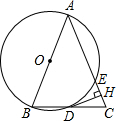 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
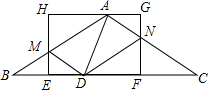 如图,在等腰三角形ABC中,AB=AC,点D是BC边上一点,BD<CD,点E是BD的中点,矩形EFGH的边EF在BC上,CF=AH,GH经过点A,AB、AC分别交HE、GF于点M、N.
如图,在等腰三角形ABC中,AB=AC,点D是BC边上一点,BD<CD,点E是BD的中点,矩形EFGH的边EF在BC上,CF=AH,GH经过点A,AB、AC分别交HE、GF于点M、N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 12 | C. | 12或16 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com