
(满分l4分)已知:抛物线y=x2-(a+2)x+9的顶点在坐标轴上.
(1)求a的值;
(2)若该抛物线的顶点C在x轴的正半轴上,而此抛物线与直线Y=x+9交于A,B两点,且A点在B点左侧,P为线段AB上的点(A,B两端点除外).过点P作x轴的垂线与抛物线交于点Q(可在图中画示意图).问:
①线段AB上是否存在这样的点P,使得PQ的长等于6?若存在,请求出点P的坐标;若不存在,请说明理由.
②线段AB上是否存在这样的点P,使得△ABQ∽△OAC?若存在,请求出此时点Q的坐标;若不存在,请说明理由.
(1)解:若抛物线y=x2-(a+2)x+9的顶点在y轴上,得a=2; ……2分
若抛物线y=x2 –(a+2)x+9的顶点在x轴上,由△=0,得a=4或a=-8. ……4分
(2)根据题意得a=4,此时抛物线为y= x2—6x+9. ……5分 y=x+9.
y=x+9.
解
y=x2-6x+9
 x1=0, x2=7
x1=0, x2=7
得
y1=9, y2=16.
所以A(0,9),B(7,16). ……7分
①由于点P在直线y=x+9上,因此设符合题意的点P的坐标为(t,t+9),此时对应的点Q的坐标为(t,t2-6t+9), ……9分
由题意得PQ=(t+9)-(t2-6t+9)=6,
解得t-l或6. ……11分
由题意0<t<7,点P的坐标为(1,10)或(6,15). ……12分
②设在线段AB上存在这样的点P,使得△ABQ∽△0AC,
∵∠BAQ=∠AOC=90°,分别过B,Q两点向Y轴作垂线,垂足为E,H,
由∠BAQ=90°,注意到直线y=x+9与x轴所夹的锐角为45°,
由QH=AH可求得点Q的坐标为(5,4),但显然AB:AQ≠OA:OC,
∴△ABQ与△OAC不可能相似, ……l3分
∴线段AB上不存在符合条件的点P. ……14分
解析


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
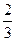 x+
x+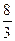 与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.
与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.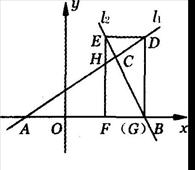
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2010年浙江省初中毕业生学业考试模拟试卷数学卷 题型:解答题
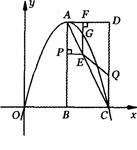
(满分l4分)如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8).抛物线y=ax2+bx过A,C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E,过点E作EF上AD交AD于点F,交抛物线于点G.当t为何值时,线段EG最长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com