
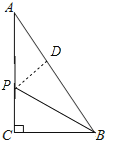
【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度向点C运动,设运动时间为t秒(t>0).
(1)若点P恰好在∠ABC的角平分线上,求出此时t的值;
(2)若点P使得PB+PC=AC时,求出此时t的值.

【答案】(1)5;(2)![]()
【解析】
(1)作PD⊥AB于D,如图,AP=t,先利用勾股定理计算出AC=8,再根据角平分线的性质得到PC=PD=8-t,利用三角形面积公式得到![]() ×10×(8-t)+
×10×(8-t)+![]() ×6×(8-t)=
×6×(8-t)=![]() ×6×8,然后解方程即可;
×6×8,然后解方程即可;
(2)先证明PB=PA=t,再利用勾股定理得到(8-t)2+62=t2,然后解方程即可.
(1)作PD⊥AB于D,如图,AP=t,
∵∠ACB=90°,AB=10,BC=6,
∴AC=![]() ,
,
∵BP平分∠ABC,
∴PC=PD=8-t,
∵S△ABP+S△BCP=S△ABC,
∴![]() ×10×(8-t)+
×10×(8-t)+![]() ×6×(8-t)=
×6×(8-t)=![]() ×6×8,
×6×8,
解得t=5,
即此时t的值为5;
(2)∵PB+PC=AC,PA+PC=AC,
∴PB=PA=t,
在Rt△BCP中,∵PC2+BC2=BP2,
∴(8-t)2+62=t2,解得t=![]() ,
,
即此时t的值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
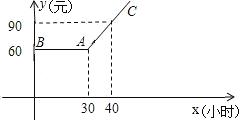
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,点
,点![]() 、
、![]() 分别是直线
分别是直线![]() 、
、![]() 上的两点.将射线
上的两点.将射线![]() 绕点
绕点![]() 顺时针匀速旋转,将射线
顺时针匀速旋转,将射线![]() 绕点
绕点![]() 顺时针匀速旋转,旋转后的射线分别记为
顺时针匀速旋转,旋转后的射线分别记为![]() 、
、![]() ,已知射线
,已知射线![]() 、射线
、射线![]() 旋转的速度之和为6度/秒.
旋转的速度之和为6度/秒.

(1)射线![]() 先转动
先转动![]() 得到射线
得到射线![]() ,然后射线
,然后射线![]() 、
、![]() 再同时旋转10秒,此时射线
再同时旋转10秒,此时射线![]() 与射线
与射线![]() 第一次出现平行.求射线
第一次出现平行.求射线![]() 、
、![]() 的旋转速度;
的旋转速度;
(2)若射线![]() 、
、![]() 分别以(1)中速度同时转动
分别以(1)中速度同时转动![]() 秒,在射线
秒,在射线![]() 与射线
与射线![]() 重合之前,设射线
重合之前,设射线![]() 与射线
与射线![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,如图2所示.
,如图2所示.
①当![]() 时,求
时,求![]() 、
、![]() 、
、![]() 满足的数量关系;
满足的数量关系;
②当![]() 时,求
时,求![]() 和
和![]() 满足的数量关系.
满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一副三角板如图甲放置,其中∠ACB=DEC=90°,∠A=45°,∠D=30°,AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D′CE′,如图乙,这时AB与CD′相交于点O,D′E′与AB、CB分别相交于点F、G,连接AD′.

(1)求∠OFE′的度数;
(2)求线段AD′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,求证:
,求证:![]() ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:
①∴![]() ,这与三角形内角和为
,这与三角形内角和为![]() 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴![]() ,③假设在
,③假设在![]() 中,
中,![]() ,④由
,④由![]() ,得
,得![]() ,即
,即![]() .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )
A.③④②①B.③④①②C.①②③④D.④③①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图:

(1)如图甲,以点O为中心,把点P顺时针旋转45°;
(2)如图乙,以点O为中心,把线段AB逆时针旋转90°;
(3)如图丙,以点O为中心,把△ABC顺时针旋转120°;
(4)如图丁,以点B为中心,把△ABC旋转180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在⊙O中,AB= 4![]() ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.

⑴求图中阴影部分的面积;
⑵若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥底面圆的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com