已知：如图，从
ABCD的顶点A、B、C、D向形外的任意直线MN引垂线
、
、
、
，垂足是
，
，
，
．求证：
＋
＝
＋
．
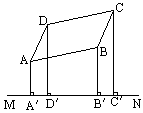
如将直线MN向上移动，使得A点在直线的一侧，B、C、D三点在直线的另一例，如图，这时，从A、B、C、D向直线MN作垂线，垂足为
、
、
、
，那么垂线段
、
、
、
之间存在什么关系？
如将直线MN再向上移动，使两侧各有两个顶点，如图，从A、B、C、D向直线MN作的垂线段
、
、
、
之间又有什么关系？写出你的猜想，并给以证明．
同步练习强化拓展系列答案科目：初中数学 来源： 题型：
查看答案和解析>>
科目：初中数学 来源： 题型：
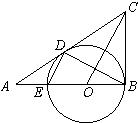27、已知：如图，在△ABC中，∠ABC=90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，连接DB，DE，OC．查看答案和解析>>
科目：初中数学 来源： 题型：
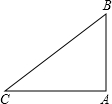A开始沿AB边向点B，再沿BC边向点C匀速移动．若P、Q两点同时从点A出发，则可同时到达点C．| 12 | 5 |
查看答案和解析>>
科目：初中数学 来源： 题型：
已知：如图，在△ABC中，∠B=90°，AB=5cm，BC=7cm．点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动．查看答案和解析>>
科目：初中数学 来源： 题型：
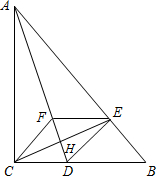（2012•鼓楼区二模）已知：如图，在△ABC中，∠ACB=90°，AD平分∠CAB，DE⊥AB，垂足为E，CD=ED．连接CE，交AD于点H． 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
⊥MN交MN于
．
中，
∥
∥
，AO＝CO，∴
是梯形
的中位线，
＝
(
＋
)．
中，
＝
(
＋
)．
＋
＝
＋
．
∥MN，使得平行四边形ABCD的四个顶点在
，
，
，
的延长线分别交
于
，
，
，
．
，
，
，
分别垂直MN于
，
，
，
，
，
，
，
分别垂直MN于
，
，
，
，且
＝
＝
＝
．
＋
＝
＋
，
－
)＋(
＋
)＝(
)＋(
＋
)，
ABCD外，类似于(1)，可证得
