
【题目】如图所示是一张简易活动餐桌,测得OA=OB=30cm,OC=OD=50cm,现要求桌面离地面的高度为40cm,那么两条桌脚的张角∠COD的度数大小应为( )
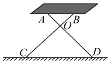
A. 100° B. 120° C. 135° D. 150°
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求PA+PB的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,正方形ABCD和一个圆心角为45°的扇形,圆心与A点重合,此扇形绕A点旋转时,两半径分别交直线BC、CD于点P.K.
(1)当点P、K分别在边BC.CD上时,如图(1),求证:BP+DK=PK.
(2)当点P、K分别在直线BC.CD上时,如图(2),线段BP、DK、PK之间又有怎样的数量关系,请直接写出结论.
(3)在图(3)中,作直线BD交直线AP、AK于M、Q两点.若PK=5,CP=4,求PM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.

(1)在图中画出四边形AB′C′D′;
(2)填空:△AC′D′是 三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表显示了同学们用计算机模拟随机投针实验的某次实验的结果.
投针次数n | 1000 | 2000 | 3000 | 4000 | 5000 | 10000 | 20000 |
针与直线相交的次数m | 454 | 970 | 1430 | 1912 | 2386 | 4769 | 9548 |
针与直线相交的频率p=
| 0.454 | 0.485 | 0.4767 | 0.478 | 0.4772 | 0.4769 | 0.4774 |
下面有三个推断:
①投掷1000次时,针与直线相交的次数是454,针与直线相交的概率是0.454;
②随着实验次数的增加,针与直线相交的频率总在0.477附近,显示出一定的稳定性,可以估计针与直线相交的概率是0.477;
③若再次用计算机模拟此实验,则当投掷次数为10000时,针与直线相交的频率一定是0.4769.
其中合理的推断的序号是:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
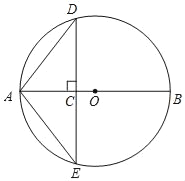
【题目】如图,⊙O的直径AB=4cm,点C为线段AB上一动点,过点C作AB的垂线交⊙O于点D,E,连结AD,AE.设AC的长为xcm,△ADE的面积为ycm2.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)确定自变量x的取值范围是 ;
(2)通过取点、画图、测量、分析,得到了y与x的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm2 | 0 | 0.7 | 1.7 | 2.9 |
| 4.8 | 5.2 | 4.6 | 0 |
(3)如图,建立平面直角坐标系xOy,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
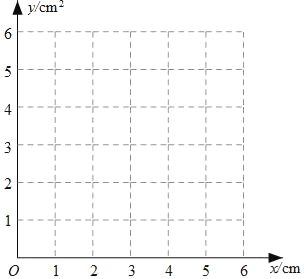
(4)结合画出的函数图象,解决问题:当△ADE的面积为4cm2时,AC的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
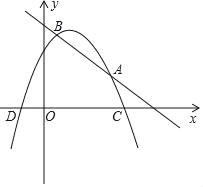
【题目】已知抛物线y=﹣x2+bx+c与直线y=﹣x+m相交于第一象限内不同的两点A(4,n),B(1,4),
(1)求此抛物线的解析式.
(2)抛物线上是否存点P,使直线OP将线段AB平分?若存在直接求出P点坐标;若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
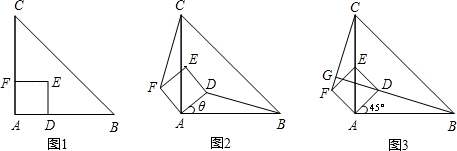
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF;
②当AB=4,AD=![]() 时,求线段BG的长.
时,求线段BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com