
【题目】在平面直角坐标系中,已知点![]() ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点![]() 的坐标。
的坐标。
(1)点![]() 在
在![]() 轴上;
轴上;
(2)点![]() 横坐标比纵坐标大3;
横坐标比纵坐标大3;
(3)点![]() 在过
在过![]() 点,且与
点,且与![]() 轴平行的直线上。
轴平行的直线上。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,如果BD,CE分别是∠ABC,∠ACB的平分线且他们相交于点P,设∠A=n°.

(1)求∠BPC的度数(用含n的代数式表示),写出推理过程.
(2)当∠BPC=125°时,∠A= .
(3)当n=60°时,EB=7,BC=12,DC的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
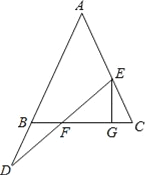
【题目】如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
(1)下列两个关系式:①DB=EC,②DF=EF,请你选择一个做为条件,另一个做为结论构成一个正确的命题,并给予证明.
你选择的条件是 ,结论是 .(只需填序号)
(2)在(1)的条件下,求证:FG=BC/2.
查看答案和解析>>
科目:初中数学 来源: 题型:
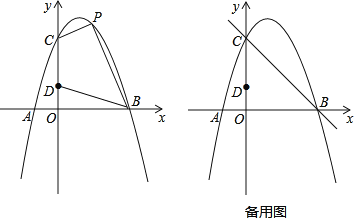
【题目】如图,对称轴为直线x=1的抛物线经过A(﹣1,0)、C(0,3)两点,与x轴的另一个交点为B,点D在y轴上,且OB=3OD
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点P的横坐标为t
①当0<t<3时,求四边形CDBP的面积S与t的函数关系式,并求出S的最大值;
②点Q在直线BC上,若以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,请求出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明![]() ;
;

【简单应用】
(2)阅读下面的内容,并解决后面的问题:如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;

解:∵AP、CP分别平分∠BAD. ∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得: ![]()
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P =![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
【问题探究】如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想![]() 的度数,并说明理由.
的度数,并说明理由.

【拓展延伸】
① 在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),

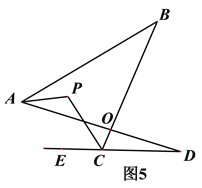
②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的一组对边AD、BC的延长线交于点E.
(1)如图①,若∠ABC=∠ADC=90°,求证:ED·EA=EC·EB;
(2)如图②,若∠ABC=120°,cos∠ADC=![]() ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
(3)如图③,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC=![]() ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).
,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在2013年义务教育质量监测过程中,为了解学生的家庭教育情况,就八年级学生平时主要和谁在一起生活进行了抽样调查.下面是根据这次调查情况制作的不完整的频数分布表和扇形统计图.

频数分布表
代码 | 和谁一起生活 | 频数 | 频率 |
A | 父母 | 4200 | 0.7 |
B | 爷爷奶奶 | 660 | a |
C | 外公外婆 | 600 | 0.1 |
D | 其它 | b | 0.09 |
合计 | 6000 | 1 |
请根据上述信息,回答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,和外公外婆一起生活的学生所对应扇形圆心角的度数是 ;
(3)若该市八年级学生共有3万人,估计不与父母一起生活的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.

(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B,C的坐标分别为A(a,3),B(b,6),C(m+6,1),且a,b满足![]()

(1)请用含m的式子表示A,B两点的坐标;
(2)如图,点A在第二象限,点B在第一象限,连接A、B、C、O四点;
①若点B到y轴的距离不小于点A到y轴距离的2倍,试求m的取值范围;
②若三角形AOC的面积等于三角形ABC面积的![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com