
 如图,⊙D与x轴相交于A(-2,0),B(-8,0),与y轴相切于C,则圆心D的坐标为(-5,4).
如图,⊙D与x轴相交于A(-2,0),B(-8,0),与y轴相切于C,则圆心D的坐标为(-5,4). 分析 作DH⊥AB与H,连结DC,DB,如图,根据垂径定理得AH=BH=$\frac{1}{2}$AB=3,则OH=OA+AH=5,再根据切线的性质得DC⊥y轴,所以四边形OCDH为矩形,则DC=OH=5,于是BD=5,然后在Rt△BDH中利用勾股定理计算出DH=4,再根据第二象限点的坐标特征写出D点坐标.
解答 解:作DH⊥AB与H,连结DC,DB,如图,
∵A(-2,0),B(-8,0),
∴OA=2,AB=-2-(-8)=6,
∵DH⊥AB,
∴AH=BH=$\frac{1}{2}$AB=3,
∴OH=OA+AH=2+3=5,
∵⊙D与y轴相切于C,
∴DC⊥y轴,
∴四边形OCDH为矩形,
∴DC=OH=5,
∴BD=5,
在Rt△BDH中,DH=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴D点坐标为(-5,4).
故答案为(-5,4).
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了坐标与图形性质、勾股定理和垂径定理.


科目:初中数学 来源: 题型:解答题
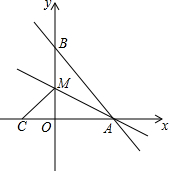 如图,在平面直角坐标系中,直线AB与x,y轴分别交于A,B两点,OB=8,OA=6,M是OB上一点,将△ABM沿AM折叠,点B恰好落在x轴上的点C
如图,在平面直角坐标系中,直线AB与x,y轴分别交于A,B两点,OB=8,OA=6,M是OB上一点,将△ABM沿AM折叠,点B恰好落在x轴上的点C查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正四棱柱的底面边长为4cm,侧棱长为8cm,一只蚂蚁从正四棱柱底面上的顶点A沿棱柱的表面到顶点C′处吃食物,那么蚂蚁走最短路线的路径为8$\sqrt{2}$cm.
如图,正四棱柱的底面边长为4cm,侧棱长为8cm,一只蚂蚁从正四棱柱底面上的顶点A沿棱柱的表面到顶点C′处吃食物,那么蚂蚁走最短路线的路径为8$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,点E是CD延长线上一点,BE与AD交于点F,若CD=2DE,且△DEF的面积为3,则三角形ABF的面积为( )
如图,在平行四边形ABCD中,点E是CD延长线上一点,BE与AD交于点F,若CD=2DE,且△DEF的面积为3,则三角形ABF的面积为( )| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7.
如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
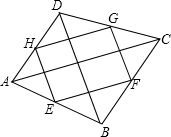 我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,如图,E、F、G、H分别是四边形ABCD各边的中点,可证中点四边形EFGH是平行四边形,如果我们对四边形ABCD的对角线AC与BD添加一定的条件,则可使中点四边形EFGH成为特殊的平行四边形,请你经过探究后回答下面问题?
我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,如图,E、F、G、H分别是四边形ABCD各边的中点,可证中点四边形EFGH是平行四边形,如果我们对四边形ABCD的对角线AC与BD添加一定的条件,则可使中点四边形EFGH成为特殊的平行四边形,请你经过探究后回答下面问题?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com