
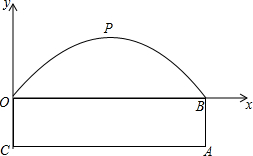
 如图所示,某隧道横截面的轮廓线由抛物线对称的一部分和矩形的一部分组成,最大高度为6米,底部宽度为12米,OC=3米,现如图建立平面直角坐标系.
如图所示,某隧道横截面的轮廓线由抛物线对称的一部分和矩形的一部分组成,最大高度为6米,底部宽度为12米,OC=3米,现如图建立平面直角坐标系.分析 (1)观察图形,根据最大高度为6米,底部宽度为12米,可得出P的坐标.
(2)已知B,P的坐标,易求出这条抛物线的函数解析式.
(2)将x=3.5代入(2)中的函数式求y的值,再与4m进行比较即可求解.
解答 解:(1)由题意得:B(12,0),P(6,3);
(2)由顶点P(6,3)设此函数解析式为:y=a(x-6)2+3,
将点(12,0)代入得a=-$\frac{1}{12}$,
∴y=-$\frac{1}{12}$(x-6)2+3;
(3)因为隧道内的路面为双车道,中间有一宽1米的隔离带,货车宽为2米,
所以当x=3.5时,代入y=-$\frac{1}{12}$(3.5-6)2+3=2$\frac{23}{48}$,
∵3+2$\frac{23}{48}$>4,
∴能通过.
点评 本题考查了二次函数的应用:构建二次函数模型解决实际问题,利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
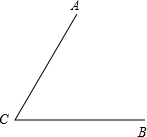 如图两条公路CA与CB,B,C是两个村庄,现在要建一个菜场,使它到两个村庄的距离相等而且还要使它到两条公路的距离也相等,用尺规作图画出菜场的位置(不写作法)保留作图痕迹.
如图两条公路CA与CB,B,C是两个村庄,现在要建一个菜场,使它到两个村庄的距离相等而且还要使它到两条公路的距离也相等,用尺规作图画出菜场的位置(不写作法)保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{8}{5}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
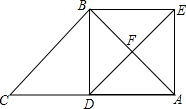 如图,已知:在△ABC中,∠ABC=90°,AB=BC=2,D是边AC上一点(D与A,C不重合),过点A作AE垂直AC,且满足AE=CD.交边AB于点F.
如图,已知:在△ABC中,∠ABC=90°,AB=BC=2,D是边AC上一点(D与A,C不重合),过点A作AE垂直AC,且满足AE=CD.交边AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com