
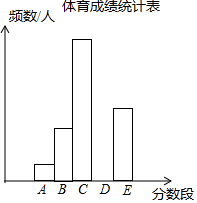
 为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.
为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.| 分数段 | A | B | C | D | E | 合计 |
| 频数/人 | 12 | 36 | 84 | b | 48 | c |
| 频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
分析 (1)首先用12÷0.05即可得到抽取的部分学生的总人数,然后用36除以总人数得到a,用总人数乘以0.25即可求出b;根据表格的信息就可以补全频数分布直方图;
(2)根据众数的定义和表格信息就可以得到这组数据的“众数”落在哪一组,进而判断小明的说法是否正确;
(3)利用30000乘以抽查的人数中优秀的学生人数所占的频率即可
解答 解:(1)∵抽取的部分学生的总人数为c=12÷0.05=240(人),
∴a=36÷240=0.15,b=240×0.25=60;
统计图补充如下: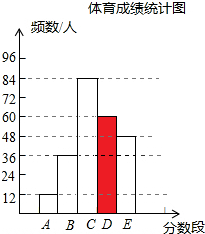
故答案是:0.15;60;240;
(2)C组数据范围是24.5~26.5,由于成绩均为整数,所以C组的成绩为25分与26分,虽然C组人数最多,但是25分与26分的人数不一定最多,所以这组数据的众数不一定在C中.故小明的说法错误;
故答案是:错误;
(3)30000×(0.25+0.20)=13500(人).
即该市今年30000名九年级学生中体育成绩为优秀的学生人数约有13500人.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.同时考查了众数的定义及用样本估计总体的思想.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+5x-1=x(x+5)-1 | B. | x2+3x-4=x(x+3-$\frac{4}{x}$) | C. | x2-9=(x+3)(x-3) | D. | (x+2)(x-2)=(x-2)(x+2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,则四边形OCED的面积为2$\sqrt{3}$.
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,则四边形OCED的面积为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 总金额($) | $10 | $5 | $5 | $2 |
| $10 | 20 | 15 | 15 | 12 |
| $5 | 15 | 10 | 10 | 7 |
| $5 | 15 | 10 | 10 | 7 |
| $2 | 12 | 7 | 7 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (5,-1) | B. | (-1,-1) | C. | (5,7) | D. | (-1,7) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com