
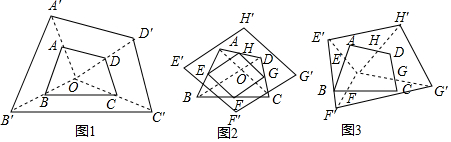
·ÖÎö Łš1Ł©žùŸĘÈęœÇĐÎÖĐλÏ߶šÀíŁŹżÉ”Ă$\frac{AB}{A'B'}$=$\frac{1}{2}$ŁŹÔÙžùŸĘËıßĐÎABCDÓëËıßĐÎA'B'C'D'ÊÇλËÆÍŒĐÎŁŹÇÒλËƱÈÎȘ$\frac{1}{2}$ŁŹŒŽżÉ”Ă”œSËıßĐÎAĄäBĄäCĄäDĄä=1ĄÁ4=4Ł»
Łš2Ł©ÁŹœÓBDŁŹBHŁŹžùŸĘEĄąFĄąGĄąH·Ö±đÊÇABĄąBCĄąCDĄąDA±ß”ÄÖД㣏żÉ”ĂSĄśAEH=$\frac{1}{2}$SĄśABH=$\frac{1}{2}$ĄÁ$\frac{1}{2}$SĄśABD=$\frac{1}{4}$SĄśABD ŁŹSĄśCFG=$\frac{1}{4}$SĄśCBD ŁŹSĄśDHG+SĄśBEF=$\frac{1}{4}$SËıßĐÎABCD ŁŹœű¶ű”Ă”œSËıßĐÎEFGH=Łš1-$\frac{1}{4}$ĄÁ2Ł©SËıßĐÎABCD=$\frac{1}{2}$ĄÁ1=$\frac{1}{2}$ŁŹÔÙžùŸĘŁš1Ł©ÖĐœáÂÛżÉÖȘŁŹSËıßĐÎEĄäFĄäGĄäHĄä=4SËıßĐÎEFGH=4ĄÁ$\frac{1}{2}$=2Ł»
Łš3Ł©ÔËÓĂŁš2Ł©ÖДķœ·šŁŹÏÈÇó”ĂSËıßĐÎEFGH=$\frac{{x}^{2}-2x+2}{{x}^{2}}$ŁŹÔÙžùŸĘSËıßĐÎEĄäFĄäGĄäHĄä=4SËıßĐÎEFGHœűĐĐŒÆËăŒŽżÉŁź
œâŽđ  œâŁșŁš1Ł©žùŸĘ¶ÔłÆĐԿɔãŹ”ăAÊÇOA'”ÄÖД㣏”ăBʱOB'”ÄÖД㣏
œâŁșŁš1Ł©žùŸĘ¶ÔłÆĐԿɔãŹ”ăAÊÇOA'”ÄÖД㣏”ăBʱOB'”ÄÖД㣏
ĄàABÊÇĄśA'B'O”ÄÖĐλÏߣŹ
Ąà$\frac{AB}{A'B'}$=$\frac{1}{2}$ŁŹ
ÓÉÌâżÉ”ĂŁŹËıßĐÎABCDÓëËıßĐÎA'B'C'D'ÊÇλËÆÍŒĐÎŁŹÇÒλËƱÈÎȘ$\frac{1}{2}$ŁŹ
ĄàËıßĐÎAĄäBĄäCĄäDĄä”ÄĂæ»ę”ÈÓÚËıßĐÎABCD”ÄĂæ»ę”Ä4±¶ŁŹ
ĄàSËıßĐÎAĄäBĄäCĄäDĄä=1ĄÁ4=4ŁŹ
čÊŽđ°žÎȘŁș4Ł»
Łš2Ł©ÈçÍŒ2ŁŹÁŹœÓBDŁŹBHŁŹ
ĄßEĄąFĄąGĄąH·Ö±đÊÇABĄąBCĄąCDĄąDA±ß”ÄÖД㣏
ĄàSĄśAEH=$\frac{1}{2}$SĄśABH=$\frac{1}{2}$ĄÁ$\frac{1}{2}$SĄśABD=$\frac{1}{4}$SĄśABD ŁŹ
ÍŹÀíŁŹSĄśCFG=$\frac{1}{4}$SĄśCBD ŁŹ
ĄàSĄśAEH+SĄśCFG=$\frac{1}{4}$ŁšSĄśABD+SĄśCBDŁ©=$\frac{1}{4}$SËıßĐÎABCD ŁŹ
ÍŹÀíżÉ”ĂŁŹSĄśDHG+SĄśBEF=$\frac{1}{4}$SËıßĐÎABCD ŁŹ
ĄàSËıßĐÎEFGH=Łš1-$\frac{1}{4}$ĄÁ2Ł©SËıßĐÎABCD=$\frac{1}{2}$ĄÁ1=$\frac{1}{2}$ŁŹ
ÓÉŁš1Ł©żÉÖȘŁŹSËıßĐÎEĄäFĄäGĄäHĄä=4SËıßĐÎEFGH=4ĄÁ$\frac{1}{2}$=2ŁŹ
čÊŽđ°žÎȘŁș$\frac{1}{2}$ŁŹ2Ł»
Łš3Ł©ÈçÍŒ3ŁŹ”ăEĄäŁŹFĄäŁŹGĄäŁŹHĄäŒŽÎȘËùÇóŁŹ
ÈçÍŒ4ŁŹÁŹœÓEFŁŹFGŁŹGHŁŹHEŁŹÁŹœÓBDŁŹBHŁŹ
Ąß$\frac{AE}{AB}$=$\frac{BF}{BC}$=$\frac{CG}{CD}$=$\frac{DH}{DA}$=$\frac{1}{x}$ŁŹ
ĄàSĄśAEH=$\frac{1}{x}$SĄśABH=$\frac{1}{x}$ĄÁ$\frac{x-1}{x}$SĄśABD=$\frac{x-1}{{x}^{2}}$SĄśABD ŁŹ
ÍŹÀíŁŹSĄśCFG=$\frac{x-1}{{x}^{2}}$SĄśCBD ŁŹ
ĄàSĄśAEH+SĄśCFG=$\frac{x-1}{{x}^{2}}$ŁšSĄśABD+SĄśCBDŁ©=$\frac{x-1}{{x}^{2}}$SËıßĐÎABCD ŁŹ
ÍŹÀíżÉ”ĂŁŹSĄśDHG+SĄśBEF=$\frac{x-1}{{x}^{2}}$SËıßĐÎABCD ŁŹ
ĄàSËıßĐÎEFGH=Łš1-$\frac{x-1}{{x}^{2}}$ĄÁ2Ł©SËıßĐÎABCD=$\frac{{x}^{2}-2x+2}{{x}^{2}}$ĄÁ1=$\frac{{x}^{2}-2x+2}{{x}^{2}}$ŁŹ
ÓÉŁš1Ł©żÉÖȘŁŹSËıßĐÎEĄäFĄäGĄäHĄä=4SËıßĐÎEFGH=4ĄÁ$\frac{{x}^{2}-2x+2}{{x}^{2}}$=$\frac{4{x}^{2}-8x+8}{{x}^{2}}$ŁŹ
čÊŽđ°žÎȘŁș$\frac{4{x}^{2}-8x+8}{{x}^{2}}$Łź
”ăÆÀ ±ŸÌâÖśÒȘżŒČéÁËÖĐ”ăËıßĐÎÒÔŒ°Î»ËÆÍŒĐΔÄĐÔÖÊ”ÄÔËÓĂŁŹœâŸöÎÊÌâ”ÄčŰŒüÊÇœ«ÍŒĐÎœűĐз֞ÀûÓĂ”È”Ś”Èžß”ÄÈęœÇĐΔÄĂæ»ę±ÈŸÍ”ÈÓÚ¶ÔÓŠ”Ś”ıȜűĐĐŒÆË㣟œâÌâʱŚąÒâŁșÏàËƶà±ßĐΔÄĂæ»ęÖź±È”ÈÓÚÏàËƱȔÄÆœ·œŁź


 ĐÂËŒÎŹŒÙÆÚŚśÒ”șźŒÙŒȘÁÖŽóѧłö°æÉçÏ”ÁĐŽđ°ž
ĐÂËŒÎŹŒÙÆÚŚśÒ”șźŒÙŒȘÁÖŽóѧłö°æÉçÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | 2Łș3 | BŁź | 8Łș5 | CŁź | 10Łș1 | DŁź | 5Łș8 |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
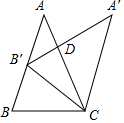 ÈçÍŒŁŹÔÚĄśABCÖĐŁŹAB=ACŁŹœ«ĄśABCÈÆ”ăCËłÊ±ŐëĐęŚȘșó”Ă”œĄśA'B'CŁŹÉèĄÏA'CB=aŁŹ”ăB'ÔÚABÉÏŁŹÔòĄÏADA'=4ŠÁ-360ĄăŁšÓĂșŹa”ÄÊœŚÓ±íÊŸŁ©
ÈçÍŒŁŹÔÚĄśABCÖĐŁŹAB=ACŁŹœ«ĄśABCÈÆ”ăCËłÊ±ŐëĐęŚȘșó”Ă”œĄśA'B'CŁŹÉèĄÏA'CB=aŁŹ”ăB'ÔÚABÉÏŁŹÔòĄÏADA'=4ŠÁ-360ĄăŁšÓĂșŹa”ÄÊœŚÓ±íÊŸŁ©Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
 ÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹŐę±ÈÀęșŻÊęy=2xÓë·Ž±ÈÀęșŻÊęy=$\frac{k}{x}$ŁškĄÙ0Ł©Ïàœ»ÓÚAĄąBÁœ”㣏ÒŃÖȘ”ăA”ÄŚű±êÊÇŁš1ŁŹaŁ©ŁŹÁíÓĐÒ»ŽÎșŻÊęy=mx+nŁšmĄÙ0Ł©”ÄÍŒÏóŸčę”ăAŁŹœ»xÖáÓÚ”ăCŁŹœ»yÖáÓÚ”ăDŁŹOC=$\sqrt{5}$OAŁź
ÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹŐę±ÈÀęșŻÊęy=2xÓë·Ž±ÈÀęșŻÊęy=$\frac{k}{x}$ŁškĄÙ0Ł©Ïàœ»ÓÚAĄąBÁœ”㣏ÒŃÖȘ”ăA”ÄŚű±êÊÇŁš1ŁŹaŁ©ŁŹÁíÓĐÒ»ŽÎșŻÊęy=mx+nŁšmĄÙ0Ł©”ÄÍŒÏóŸčę”ăAŁŹœ»xÖáÓÚ”ăCŁŹœ»yÖáÓÚ”ăDŁŹOC=$\sqrt{5}$OAŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | $\sqrt{-x-2}$ | BŁź | $\sqrt{x}$ | CŁź | $\sqrt{{x}^{2}+2}$ | DŁź | $\sqrt{-5}$ |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | 2x+1=0 | BŁź | y2+x=0 | CŁź | x2-x=0 | DŁź | $\frac{1}{x}$+x2=0 |
Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com