
【题目】已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.
(1)如图①,若∠COF=34°,则∠BOE=________;若∠COF=m°,则∠BOE=________,∠BOE与∠COF的数量关系式为________;
(2)当射线OE绕点O逆时针旋转到如图②的位置时,(1)中∠BOE与∠COF的数量关系是否成立?请说明理由.
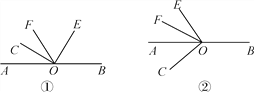
【答案】(1)68°,2m°,∠BOE=2∠COF;(2)成立,理由见解析.
【解析】(1)由∠COF=34°,∠COE是直角,易求∠EOF,而OE平分∠AOE,可求∠AOE,进而可求∠BOE,若∠COF=m°,则∠BOE=2m°;进而可知∠BOE=2∠COF;
(2)由于∠COE是直角,于是∠EOF=90°-∠COF,而OF平分∠AOE,则有∠AOE=2∠EOF,从而可得∠BOE=180°-∠AOE=180°-2(90°-∠COF)=2∠COF.
解:(1)∵∠COF=34°,∠COE是直角,
∴∠EOF=90°-34°=56°,
又∵OF平分∠AOE,
∴∠AOE=2∠EOF=112°,
∴∠BOE=180°-112°=68°,
若∠COF=m°,则∠BOE=2m°;
故∠BOE=2∠COF;
故答案是68°;2m°;∠BOE=2∠COF;
(2)∠BOE和∠COF的关系依然成立.
∵∠COE是直角,
∴∠EOF=90°-∠COF,
又∵OF平分∠AOE,
∴∠AOE=2∠EOF,
∴∠BOE=180°-∠AOE=180°-2(90°-∠COF)=2∠COF.
“点睛”本题考查了角的计算.解题的关键是注意找出所求角与已知角之间的关系,例如:互余、互补关系.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】下列条件中,不能确定两个三角形全等的条件是( )
A.三条边对应相等
B.两角和其中一角的对边对应相等
C.两角和它们的夹边对应相等
D.两边和一角对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD,AB=9,AD=4. E为CD边上一点,CE=6.
(1)求AE的长.
(2)点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE. 设点P运动的时间为t秒,则当t为何值时,△PAE为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察探索:
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(x﹣1)(x4+x3+x2+x+1)=x5﹣1
根据规律填空:(x﹣1)(xn+xn﹣1+…+x+1)=__.(n为正整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com