
将连续的自然数1~1001按下面的方式排列成一个长正方形数阵,用一个正方形框出16个数,要使这个正方形框出的16个数之和分别等于(1)1998;(2)1991;(3)2000;(4)2080.这是否可能?试说明理由.若有可能,请写出该方框内的16个数中的最小数与最大数.

|
解:设框内左上角的数字为x,则其余15个数字分别为x+1,x+2,x+3,x+7,x+8,x+9,x+10,x+14,x+15,x+16,x+17,x+21,x+22,x+23,x+24. 这16个数字的和为16x+192. 当和为1998时,x无整数解; 当和为1991时,x也无整数解; 当和为2000时,x=113; 当和为2080时,x=118. 而当x=113时,113÷7=16余1,即113是第17排第1个数,该方框内的最大数为113+24=137; 当x=118时,118÷7=16余6,即118是第17排第6个数,故方框内不能框得各数之和为2080. |


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:初中数学 来源: 题型:
 27、将连续的自然数1至36按如图的方式排成一个正方形阵列,用一个小正方形任意圈出其中的9个数,设圈出的9个数的中心的数为a,用含有a的代数式表示这9个数的和为
27、将连续的自然数1至36按如图的方式排成一个正方形阵列,用一个小正方形任意圈出其中的9个数,设圈出的9个数的中心的数为a,用含有a的代数式表示这9个数的和为查看答案和解析>>
科目:初中数学 来源: 题型:
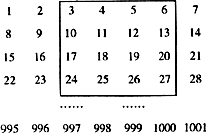 将连续的自然数1-1001按如上图的方式排列成一个长方形阵列,用一个正方形框出16个数,若这个正方形框出的16个数的和为2016,请写出该方框16个数中的最小数与最大数之和是
将连续的自然数1-1001按如上图的方式排列成一个长方形阵列,用一个正方形框出16个数,若这个正方形框出的16个数的和为2016,请写出该方框16个数中的最小数与最大数之和是查看答案和解析>>
科目:初中数学 来源: 题型:
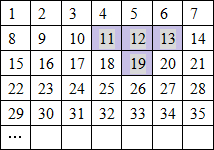 将连续的自然数1,2,3,4,5,6,7,8,9…,排成如图所示的数阵.“T”型浅色方框里的四个数的和是55,不改变方框的大小,移动方框,使方框里的四个数的和等于2007,那么在方框里的四个数中,最小的是
将连续的自然数1,2,3,4,5,6,7,8,9…,排成如图所示的数阵.“T”型浅色方框里的四个数的和是55,不改变方框的大小,移动方框,使方框里的四个数的和等于2007,那么在方框里的四个数中,最小的是查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com