
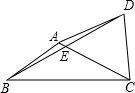
 如图,在四边形ABCD中,对角线AC、BD交于点E,点E为BD的中点,∠BAC+∠BDC=180°,AB=CD=5,tan∠ACB=$\frac{1}{2}$,则AD=2$\sqrt{10}$.
如图,在四边形ABCD中,对角线AC、BD交于点E,点E为BD的中点,∠BAC+∠BDC=180°,AB=CD=5,tan∠ACB=$\frac{1}{2}$,则AD=2$\sqrt{10}$. 分析 作辅助线,构建直角三角形,证明△BME≌△DNE和Rt△ABM≌Rt△DCN,得BE=CE=DE,从而得△BCD是直角三角形,利用同角的正切先求出BC的长,再依次求出AM、CN、DN、AD的长,
解答 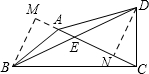 解:过B作BM⊥CA,交CA的延长线于M,过D作DN⊥CA,垂足为N,
解:过B作BM⊥CA,交CA的延长线于M,过D作DN⊥CA,垂足为N,
∴∠BME=∠DN90°,
∵点E为BD的中点,
∴BE=DE,
∵∠BEM=∠DEN,
∴△BME≌△DNE,
∴BM=DN,
∵AB=CD,
∴Rt△ABM≌Rt△DCN,
∴∠BAM=∠DCN,
∵∠BAC+∠BDC=180°,∠BAC+∠BAM=180°,
∴∠BDC=∠BAM,
∴∠BDC=∠DCN,
∴DE=CE,
∴BE=CE=DE,
∴∠DBC=∠ECB,
∴∠DBC+∠BDC=∠ECB+∠DCN,
∴△BCD是直角三角形,
∵tan∠ACB=$\frac{1}{2}$,
∴tan∠DBC=$\frac{1}{2}$,
∵DC=5,
∴BC=10,
在△BMC中,设BM=x,则CM=2x,
由勾股定理得:x2+(2x)2=102,
x=±2$\sqrt{5}$,
∴BM=DN=2$\sqrt{5}$,CM=4$\sqrt{5}$,
由勾股定理得:AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=$\sqrt{{5}^{2}-(2\sqrt{5})^{2}}$=$\sqrt{5}$,
∴CN=AM=$\sqrt{5}$,
∴AN=CM-AM-CN=4$\sqrt{5}$-$\sqrt{5}$-$\sqrt{5}$=2$\sqrt{5}$,
在△ADN中,AD=$\sqrt{A{N}^{2}+D{N}^{2}}$=$\sqrt{(2\sqrt{5})^{2}+(2\sqrt{5})^{2}}$=$\sqrt{40}$=2$\sqrt{10}$,
故答案为:2$\sqrt{10}$.
点评 本题是解直角三角形问题,恰当地构建辅助线是本题的关键,利用三角形全等证明边相等,并借助同角的三角函数值求线段的长,与勾股定理相结合,依次求出各边的长即可.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:选择题
 如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( )
如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( )| A. | AD=BD | B. | OC=2CD | C. | ∠CAD=∠CBD | D. | ∠OCA=∠OCB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x^6}{x^2}$=x3 | B. | $\frac{x+y}{x+y}$=0 | C. | $\frac{x+y}{{{x^2}+xy}}=\frac{1}{x}$ | D. | $\frac{{2x{y^2}}}{{4{x^2}y}}=\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
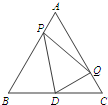 如图,△ABC是等边三角形,AB=2,D是边BC的中点.点P从点A出发,沿AB-BD以每秒1个单位长度的速度向终点D运动(点P不与点A、D重合).同时点Q从点C出发,沿CA-AC以每秒1个单位长度的速度运动.当点P停止运动时,点Q也随之停止运动.设点P的运动时间为t(秒),△PQD的面积为S.
如图,△ABC是等边三角形,AB=2,D是边BC的中点.点P从点A出发,沿AB-BD以每秒1个单位长度的速度向终点D运动(点P不与点A、D重合).同时点Q从点C出发,沿CA-AC以每秒1个单位长度的速度运动.当点P停止运动时,点Q也随之停止运动.设点P的运动时间为t(秒),△PQD的面积为S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com