
【题目】如图,AB是⊙O的直径,C是圆上一点,弦CD⊥AB于点E,且DC=AD.过点A作⊙O的切线,过点C作DA的平行线,两直线交于点F,FC的延长线交AB的延长线于点G.
(1)求证:FG与⊙O相切;
(2)连接EF,求![]() 的值.
的值.

【答案】(1)见解析;(2)![]()
【解析】(1)连接OC、AC,先证DC=AD= AC,得出△ACD为等边三角形,所以∠D =∠DCA=∠DAC =60°,从而FG∥DA,易知![]() , 得出FG⊥OC ,则FG与⊙O相切;(2)作EH⊥FG于点H.设CE= a,则DE= a,AD=2a,易证四边形AFCD为平行四边形,因为DC =AD,AD=2a,所以 四边形AFCD为菱形,由(1)得∠DCG=60°,从而可求出EH、CH的值,然后可知FH的长度,利用锐角三角函数的定义即可求出tan∠EFC的值.
, 得出FG⊥OC ,则FG与⊙O相切;(2)作EH⊥FG于点H.设CE= a,则DE= a,AD=2a,易证四边形AFCD为平行四边形,因为DC =AD,AD=2a,所以 四边形AFCD为菱形,由(1)得∠DCG=60°,从而可求出EH、CH的值,然后可知FH的长度,利用锐角三角函数的定义即可求出tan∠EFC的值.
(1)证明:如图,连接OC,AC.

∵ AB是⊙O的直径,弦CD⊥AB于点E,
∴ CE=DE,AD=AC.
∵ DC=AD,
∴ DC=AD= AC.
∴ △ACD为等边三角形.
∴ ∠D =∠DCA=∠DAC =60°.
∴ ![]() .
.
∵ FG∥DA,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴ FG⊥OC.
∴ FG与⊙O相切.
(2)解:如图,作EH⊥FG于点H.
设CE= a,则DE= a,AD=2a.
∵ AF与⊙O相切,
∴ AF⊥AG.
又∵ DC⊥AG,
可得AF∥DC.
又∵ FG∥DA,
∴ 四边形AFCD为平行四边形.
∵ DC =AD,AD=2a,
∴ 四边形AFCD为菱形.
∴ AF=FC=AD=2 a,∠AFC=∠D = 60°.
由(1)得∠DCG= 60°,![]() ,
,![]() .
.
∴ ![]() .
.
∵ 在Rt△EFH中,∠EHF= 90°,
∴ 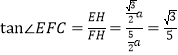 .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有a个除颜色外完全相同的红球和白球,其中红球有b个,将盒中的球摇匀后从中任意摸出1个球,记录颜色后将球放回盒中,重复进行这过程,如表记录了某班一次摸球实验情况:
摸球总数n | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
摸到红球数m | 325 | 1336 | 3203 | 6335 | 8073 | 12628 |
摸到红球的频率(精确到0.001) | 0.813 | 0.891 | 0.915 | 0.905 | 0.897 | 0.902 |
(1)由此估计任意摸出1个球为红球的概率约是 (精确到0.1)
(2)实验结束后,小明发现了一个一般性的结论:盒子中共有a个球,其中红球有b个,则摇匀后从中任意摸出1个球为红球的概率P可以表示为![]() ,这个结论也得到了老师的证实根据小明的发现,若在该盒子中再放入除颜色外与原来的球完全相同的2个红球和2个白球,摇匀后从中任意摸出1个球为红球的概率为P’,请通过计算比较P与P'的大小.
,这个结论也得到了老师的证实根据小明的发现,若在该盒子中再放入除颜色外与原来的球完全相同的2个红球和2个白球,摇匀后从中任意摸出1个球为红球的概率为P’,请通过计算比较P与P'的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=ax2-2ax+c经过点C(1,2),与x轴交于A(-1,0)、B两点
(1) 求抛物线C的解析式
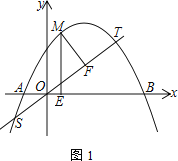
(2) 如图1,直线![]() 交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
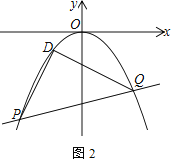
(3) 如图2,平移抛物线C的顶点到原点得抛物线C1,直线l:y=kx-2k-4交抛物线C1于P、Q两点,在抛物线C1上存在一个定点D,使∠PDQ=90°,求点D的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
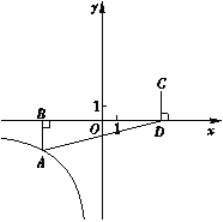
【题目】如图,在平面直角坐标系xOy中,函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
(1)求m,n的值;
(2)若直线![]() (k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当
(k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当![]() 时,求点F的坐标.
时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“一起阅读,共同成长”课外读书周活动,活动后期随机调查了八年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
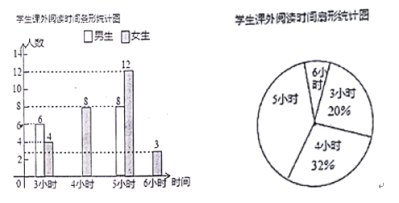
(1)本次调查的学生总数为______人,在扇形统计图中,课外阅读时间为5小时的扇形圆心角度数是______;
(2)请你补全条形统计图;
(3)若全校八年级共有学生![]() 人,估计八年级一周课外阅读时间至少为
人,估计八年级一周课外阅读时间至少为![]() 小时的学生有多少人?
小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O在直线AB上,作射线OC,点D在平面内,∠BOD与∠AOC互余.
(1)若∠AOC:∠BOD=4:5,则∠BOD= ;
(2)若∠AOC=α(0°<α≤45°),ON平分∠COD.
①当点D在∠BOC内,补全图形,直接写出∠AON的值(用含α的式子表示);
②若∠AON与∠COD互补,求出α的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求画图:(1)如图1平面上有五个点![]() ,按下列要求画出图形.
,按下列要求画出图形.
①连接![]() ;
;
②画直线![]() 交
交![]() 于点
于点![]() ;
;
③画出线段![]() 的反向延长线;
的反向延长线;
④请在直线![]() 上确定一点
上确定一点![]() ,使
,使![]() 两点到点
两点到点![]() 的距离之和最小,并写出画图的依据.
的距离之和最小,并写出画图的依据.
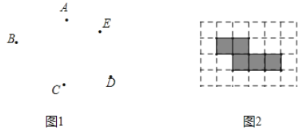
(2)有5个大小一样的正方形制成如图2所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注意:只需添加一个符合要求的正方形,并用阴影表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com