
【题目】如图,正方形![]() 的边长为4,延长
的边长为4,延长![]() 至E使
至E使![]() ,以
,以![]() 为边在上方作正方形
为边在上方作正方形![]() ,延长
,延长![]() 交
交![]() 于M,连接
于M,连接![]() ,
,![]() ,H为
,H为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() ,
,![]() 交于点N、K.则下列结论:
交于点N、K.则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正确的是______________.(填写所有正确结论的序号)
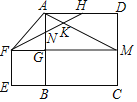
【答案】①③④
【解析】
由正方形的性质可得FG=BE-2,∠FGB=90°,AD=4,AH=2,∠BAD=90°,求得∠HAN=∠FGN,AH=FG,可证△ANH≌△GNF(AAS),故①正确;根据全等三角形的性质可得∠AHN=∠HFG,则∠AFH≠∠AH F,即 ∠AFN≠∠HFG,故②错误;根据全等三角形的性质得到![]() ,再根据相似三角形的性质可得∠AHN=∠AM G,根据平行线的性质可得∠HAK=∠AMG,最后根据直角三角形的性质可得
,再根据相似三角形的性质可得∠AHN=∠AM G,根据平行线的性质可得∠HAK=∠AMG,最后根据直角三角形的性质可得![]() ,故③正确;根据矩形的性质得到DM=AG=2,最后根据三角形的面积公式判定即可.
,故③正确;根据矩形的性质得到DM=AG=2,最后根据三角形的面积公式判定即可.
解:①∵四边形![]() 是正方形,
是正方形,![]() ,
,
∴![]() ,
,
∵四边形![]() 是正方形,H为
是正方形,H为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,故①正确;
,故①正确;
②∵△ANH≌△GNF
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,故②错误;
,故②错误;
③∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;故③正确;
;故③正确;
∵延长![]() 交
交![]() 于M,
于M,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,故④正确.
,故④正确.
故答案为①③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,过点A(1,0)作x轴的垂线与直线y=x相交于点B,以原点O为圆心、OA为半径的圆与y轴相交于点C、D,抛物线y=x2+px+q经过点B、C.
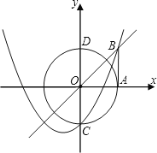
(1)求p、q的值;
(2)设抛物线的对称轴与x轴相交于点E,连接CE并延长与⊙O相交于点F,求EF的长;
(3)记⊙O与x轴负半轴的交点为G,过点D作⊙O的切线与CG的延长线相交于点H.点H是否在抛物线上?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在九年级“线上教学”结束后,为了解学生的视力情况,抽查了部分学生进行视力检测.根据检测结果,制成下面不完整的统计图表.
被抽样的学生视力情况频数表
组别 | 视力段 | 频数 |
A | 5.1≤x≤5.3 | 25 |
B | 4.8≤x≤5.0 | 115 |
C | 4.4≤x≤4.7 | m |
D | 4.0≤x≤4.3 | 52 |
(1)求组别C的频数m的值.
(2)求组别A的圆心角度数.
(3)如果视力值4.8及以上属于“视力良好”,请估计该市25000名九年级学生达到“视力良好”的人数.根据上述图表信息,你对视力保护有什么建议?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
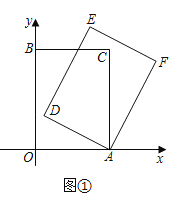
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;
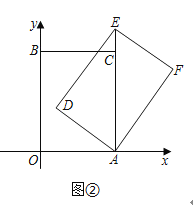
(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
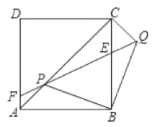
【题目】如图,边长为![]() 的正方形
的正方形![]() 中,P是对角线
中,P是对角线![]() 上的一个动点(点P与A、C不重合),连接
上的一个动点(点P与A、C不重合),连接![]() ,将
,将![]() 绕点B顺时针旋转90°到
绕点B顺时针旋转90°到![]() ,连接
,连接![]() ,
,![]() 与
与![]() 交于点E,
交于点E,![]() 延长线与
延长线与![]() (或
(或![]() 延长线)交于点F.
延长线)交于点F.
(1)连接![]() ,证明:
,证明:![]() ;
;
(2)设![]() ,试写出y关于x的函数关系式,并求当x为何值时,
,试写出y关于x的函数关系式,并求当x为何值时,![]() ;
;
(3)猜想![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
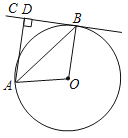
【题目】如图,AB是⊙O的弦,直线BC与⊙O相切于点B,AD⊥BC,垂足为D,连接OA,OB.
(1)求证:AB平分∠OAD;
(2)当∠AOB=100°,⊙O的半径为6cm时.
①直接写出扇形AOB的面积约为 cm2(结果精确到1cm2);
②点E是⊙O上一动点(点E不与点A、点B重合),连接AE,BE,请直接写出∠AEB= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
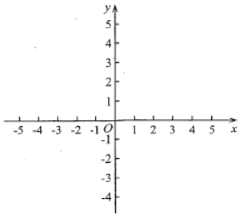
【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系![]() 中,点
中,点![]() ,
,![]() 分别在
分别在![]() 轴的正半轴和
轴的正半轴和![]() 轴的正半轴上.
轴的正半轴上.
(1)分别以点![]() ,
,![]() ,
,![]() 为圆心,
为圆心,![]() 为半径作圆,得到
为半径作圆,得到![]() ,
,![]() 和
和![]() ,其中是
,其中是![]() 的角内圆的是_______;
的角内圆的是_______;
(2)如果以点![]() 为圆心,以
为圆心,以![]() 为半径的
为半径的![]() 为
为![]() 的角内圆,且与一次函数图像
的角内圆,且与一次函数图像![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
(3)点![]() 在第一象限内,如果存在一个半径为
在第一象限内,如果存在一个半径为![]() 且过点
且过点![]() 的圆为∠EOM的角内相切圆,直接写出∠EOM的取值范围.
的圆为∠EOM的角内相切圆,直接写出∠EOM的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面贯彻党的教育方针和落实阳光体育运动,提高青少年学生身体健康水平和体育运动水平,某校准备购买一批篮球,甲、乙两家商店的标价都是每个![]() 元,两家商店推出不同的优惠方式如下表:
元,两家商店推出不同的优惠方式如下表:
商店 | 优惠方式 |
甲 | 购买数量不超过 |
乙 | 按照标价的八折销售 |
(1)设该学校购买![]() 个篮球,在甲商店购买花费
个篮球,在甲商店购买花费![]() 元,在商店购买花费
元,在商店购买花费![]() 元,请分别求出
元,请分别求出![]() 、
、![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若学校需购买![]() 个篮球,请你通过计算进行对比,选择哪家商店更省钱?
个篮球,请你通过计算进行对比,选择哪家商店更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com