
【题目】如图(a),将两块直角三角尺的直角顶点C叠放在一起.
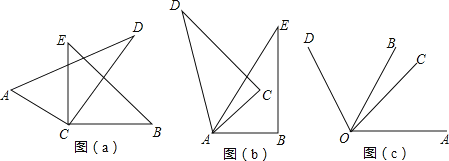
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;并猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(2)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(3)已知∠AOB=α,∠COD=β(都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小相等的关系(用含有α,β的式子表示).
【答案】(1)145°,40°,∠ACB+∠DCE=180°,理由见解析;(2)∠DAB+∠CAE=120°,理由见解析;(3)∠AOD+∠BOC=α+β.
【解析】
(1)若∠DCE=35°,根据90°计算∠ACE的度数,再计算∠ACB的度数;若∠ACB=140°,同理,反之计算可得结果;先计算∠ACB=90°+∠BCD,再加上∠DCE可得∠ACB与∠DCE的关系;
(2)先计算∠DAB=60°+∠CAB,再加上∠CAE可得结果;
(3)先计算∠AOD=β+∠COA,再加上∠BOC可得结果.
解:(1)若∠DCE=35°,
∵∠ACD=90°,∠DCE=35°,
∴∠ACE=90°35°=55°,
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°;
若∠ACB=140°,
∵∠BCE=90°,
∴∠ACE=140°90°=50°,
∵∠ACD=90°,
∴∠DCE=90°50°=40°,
故答案为:145°;40°;
∠ACB+∠DCE=180°,
理由:∵∠ACB=∠ACD+∠BCD=90°+∠BCD,
∴∠ACB+∠DCE=90°+∠BCD+∠DCE=90°+∠BCE=180°;
(2)∠DAB+∠CAE=120°,
理由:∵∠DAB=∠DAC+∠CAB=60°+∠CAB,
∴∠DAB+∠CAE=60°+∠CAB+∠CAE=60°+∠EAB=120°;
(3)∠AOD+∠BOC=α+β,
理由:∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC=β+∠AOB=α+β.


科目:初中数学 来源: 题型:
【题目】(14分)小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入2400元;
营业员B:月销售件数300件,月总收入2700元;
假设营业员的月基本工资为![]() 元,销售每件服装奖励
元,销售每件服装奖励![]() 元.
元.
(1)求![]() 、
、![]() 的值;
的值;
(2)若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 中,
中,![]() ,
,![]() 是
是![]() 边上一点,作
边上一点,作![]() ,分别交边
,分别交边![]() ,
,![]() 于点
于点![]() ,
,![]() .
.

(1)若![]() (如图1),求证:
(如图1),求证:![]() .
.
(2)若![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() (或
(或![]() 的延长线)于点
的延长线)于点![]() .试猜想:线段
.试猜想:线段![]() ,
,![]() 和
和![]() 之间的数量关系,并就
之间的数量关系,并就![]() 情形(如图2)说明理由.
情形(如图2)说明理由.
(3)若点![]() 与
与![]() 重合(如图3),
重合(如图3),![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②设![]() ,
,![]() ,
,![]() ,试证明:
,试证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体的块数最多是( )

A. 9 B. 10 C. 11 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥底面圆的圆心,圆锥的高为2![]() m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
(1)求∠ABC的度数;
(2)若∠ACP=2∠ABC,求光源A距水平面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
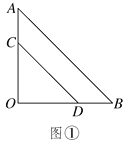
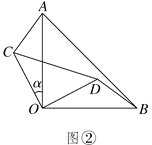
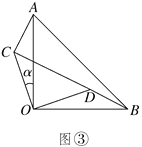
【题目】两块等腰直角三角形纸片AOB和COD按图①所示放置,直角顶点重合在点O处,AB=25.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图②所示.
(1)在图②中,求证:AC=BD,且AC⊥BD;
(2)当BD与CD在同一直线上(如图③)时,若AC=7,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
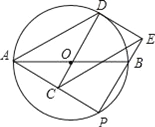
【题目】如图,AB是⊙O的直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE交AB于点F,连接DF.
(1)求证:△DAC≌△ECP;
(2)填空:
①四边形ACED是何种特殊的四边形?
②在点P运动过程中,线段DF、AP的数量关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com