
分析 设点C(0,k),分向上平移和向下平移,利用割补法和S△ABC=6建立关于k的方程,求得点C坐标,即可得出平移的方向和距离,继而由平移的性质可得答案.
解答 解:设点C(0,k),
如图1,当点C在点A上方时,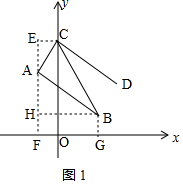
∵S△ABC=S梯形CEHB-S△AEC-S△ABH,即$\frac{1}{2}$×(1+3)×(k-1)-$\frac{1}{2}$×1×(k-4)-$\frac{1}{2}$×3×3=6,
解得:k=7,
即点C(0,7),
则线段AB需向右平移1个单位,向上平移3个单位,
∴点B(2,1)的对应点D的坐标为(3,4);
如图2,当点C在点A下方时,
∵S△ABC=S梯形AEFB-S梯形ACOE-S梯形BCOF,即$\frac{1}{2}$×(1+4)×3-$\frac{1}{2}$×(k+4)×1-$\frac{1}{2}$×(k+1)×2=6,
∴k=-1,
即点C(0,-1),
则线段AB需向右平移1个单位,向下平移5个单位,
∴点B(2,1)的对应点D的坐标为(3,6);
故答案为:(3,4)或(3,6).
点评 本题主要考查坐标与图形的变化-平移,根据割补法建立关于k的方程及分类讨论思想的运用是解题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,直线l交x轴和y轴于点A,B,反比例函数y=$\frac{8}{x}$(x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=$\frac{-6}{x}$(x<0)的图象于点E,则图中阴影部分的总面积为7.
如图,在平面直角坐标系xOy中,直线l交x轴和y轴于点A,B,反比例函数y=$\frac{8}{x}$(x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=$\frac{-6}{x}$(x<0)的图象于点E,则图中阴影部分的总面积为7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1$\frac{1}{5}$ | B. | $\frac{15}{24}$ | C. | $\frac{13}{40}$ | D. | $\frac{6}{18}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com