
【题目】甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.

(1)分别求出S甲、S乙与t的函数关系式(不必写出t的取值范围);
(2)求A、B两城之间的距离,及t为何值时两车相遇;
(3)当两车相距300千米时,求t的值.
【答案】(1)S甲=-180t+600,S乙=120t;(2)A、B两城之间的距离是600千米,t为2时两车相遇;(3)当两车相距300千米时,t的值是1或3.
【解析】
(1)根据函数图象可以分别求得S甲、S乙与t的函数关系式;
(2)将t=0代入S甲=-180t+600,即可求得A、B两城之间的距离,然后将(1)中的两个函数相等,即可求得t为何值时两车相遇;
(3)根据题意可以列出相应的方程,从而可以求得t的值.
(1)设S甲与t的函数关系式是S甲=kt+b,
![]() ,得
,得![]() ,
,
即S甲与t的函数关系式是S甲=-180t+600,
设S乙与t的函数关系式是S乙=at,
则120=a×1,得a=120,
即S乙与t的函数关系式是S乙=120t;
(2)将t=0代入S甲=-180t+600,得
S甲=-180×0+600,得S甲=600,
令-180t+600=120t,
解得,t=2,
即A、B两城之间的距离是600千米,t为2时两车相遇;
(3)由题意可得,
|-180t+600-120t|=300,
解得,t1=1,t3=3,
即当两车相距300千米时,t的值是1或3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】观察如图图形:
它们是按一定规律排列的:
(1)依照此规律,第8个图形共有__枚五角星.
(2)用代数式表示第n个图形共有___枚五角星
(3)第99个图形共有多少枚五角星?
查看答案和解析>>
科目:初中数学 来源: 题型:
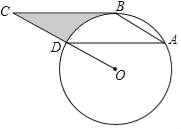
【题目】如图所示,点ABD都在⊙O上,BC是⊙O的切线,AD∥BC,∠C=30°,AD=4![]() .
.
(1)求∠A的度数;
(2)求由线段BC、CD与弧BD所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b互为相反数,c,d互为倒数,m的绝对值是1,n是有理数且既不是正数也不是负数,求20161﹣(a+b)+m![]() ﹣(cd)2016+n(a+b+c+d)的值.
﹣(cd)2016+n(a+b+c+d)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一家苗圃计划种植桃树和柏树.根据市场调查与预测,种植桃树的利润y1(万元)与投资成本x(万元)满足如图①所示的二次函数y1=ax2;种植柏树的利润y2(万元)与投资成本x(万元)满足如图②所示的正比例函数y2=kx.
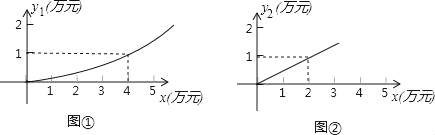
(1)分别求出利润y1(万元)和利润y2(万元)关于投资成本x(万元)的函数关系式;
(2)如果这家苗圃投入10万元资金种植桃树和柏树,苗圃至少能获得多少利润?若要使这家苗圃获得5万元利润,资金投入如何分配(桃树和柏树都要种植)?
查看答案和解析>>
科目:初中数学 来源: 题型:
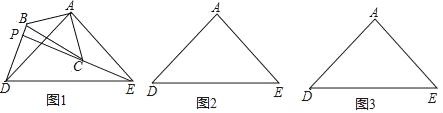
【题目】如图所示,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,EC的延长线交BD于点P.
(1)把△ABC绕点A旋转到图1,BD,CE的关系是 (选填“相等”或“不相等”);简要说明理由;
(2)若AB=3,AD=5,把△ABC绕点A旋转,当∠EAC=90°时,在图2中作出旋转后的图形,PD= ,简要说明计算过程;
(3)在(2)的条件下写出旋转过程中线段PD的最小值为 ,最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少4000元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资.加工1件A型服装计酬20元,加工1件B型服装计酬15元.在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时,加工1件A型服装和2件B型服装需4小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型商业中心开业,为吸引顾客,特在一指定区域放置一批按摩休闲椅,供顾客有偿体验,收费如下图:
(1)若在此按摩椅上连续休息了1小时,需要支付多少元?
(2)某人在该椅上一次性消费18元,那么他在该椅子上最多休息了多久?
(3)张先生到该商场会见一名客人,结果客人告知临时有事,预计4.5小时后才能到来;那么如果张先生要在该休闲椅上休息直至客人到来,他至少需要支付多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com