
【题目】计算与化简:
(1)(﹣ ![]() )×(﹣12)
)×(﹣12)
(2)(﹣3)2÷(2 ![]() )﹣4×(﹣
)﹣4×(﹣ ![]() )2
)2
(3)x2y﹣3×( ![]() xy2﹣
xy2﹣ ![]() yx2)+y2x,其中x=﹣2,y=1.
yx2)+y2x,其中x=﹣2,y=1.
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连结CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
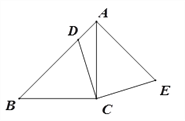
(1)求证:AB⊥AE;
(2)若![]() ,求证:四边形ADCE为正方形.
,求证:四边形ADCE为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块直角三角尺的直角顶点C叠放在一起.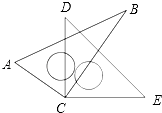
(1)写出以C为顶点的相等的锐角,并说明理由;
(2)若射线CB平分∠DCE,求∠ACE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4 , 给出如下结论:①S1+S4=S2+S3;②S2+S4=S1+S2;③若S3=2S1 , 则S4=2S2;④若S1=S2 , 则S3=S4 , 其中正确结论的序号是 . 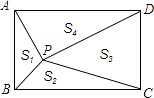
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①两点之间的所有连线中,线段最短;②相等的角是对顶角; ③过一点有且仅有一条直线与己知直线垂直; ④两点之间的距离是两点间的线段;⑤若AB=BC,则点B为线段AC的中点。其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题: 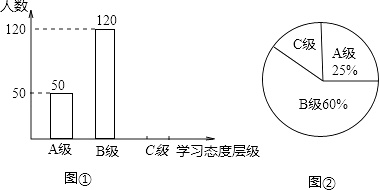
(1)此次抽样调查中,共调查了名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.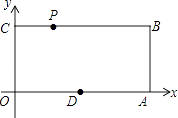
(1)△ODP的面积S= .
(2)t为何值时,四边形PODB是平行四边形?
(3)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(4)若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店用1000元购进一批套尺,很快销售一空;商店又用1500元购进第二批同款套尺,购进单价比第一批贵25%,所购数量比第一批多100套.
(1)求第一批套尺购进的单价;
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com