
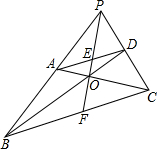
 已知:如图,AD∥BC,BD、AC交于O,BA、CD的延长线交于P,PO的延长线交BC于F.求证:
已知:如图,AD∥BC,BD、AC交于O,BA、CD的延长线交于P,PO的延长线交BC于F.求证:分析 (1)由AD∥BC,得到△PAE∽△PBF,△PDE∽△PCF,△AEO∽△COF,△DEO∽△BFO根据相似三角形的性质得到$\frac{AE}{BF}$=$\frac{PE}{PF}$,$\frac{DE}{CF}=\frac{PE}{PF}$,$\frac{AE}{CF}=\frac{OE}{OF}$,$\frac{DE}{BF}=\frac{OE}{OF}$,等量代换得到$\frac{AE}{BF}$=$\frac{DE}{CF}$,$\frac{AE}{CF}$=$\frac{DE}{BF}$,两式相除得到$\frac{\frac{DE}{CF}}{\frac{AE}{CF}}$=$\frac{\frac{AE}{BF}}{\frac{DE}{BF}}$,于是得到结论;
(2)由(1)证得:$\frac{AE}{BF}$=$\frac{DE}{CF}$,$\frac{AE}{CF}$=$\frac{DE}{BF}$,两式相除得到$\frac{\frac{AE}{BF}}{\frac{AE}{CF}}$=$\frac{\frac{DE}{CF}}{\frac{DE}{BF}}$,即$\frac{CF}{BF}$=$\frac{BF}{CF}$,即可得到结论.
解答 解:(1)∵ AD∥BC,
AD∥BC,
∴△PAE∽△PBF,△PDE∽△PCF,△AEO∽△COF,△DEO∽△BFO
∴$\frac{AE}{BF}$=$\frac{PE}{PF}$,$\frac{DE}{CF}=\frac{PE}{PF}$,$\frac{AE}{CF}=\frac{OE}{OF}$,$\frac{DE}{BF}=\frac{OE}{OF}$,
∴$\frac{AE}{BF}$=$\frac{DE}{CF}$,$\frac{AE}{CF}$=$\frac{DE}{BF}$,
∴$\frac{\frac{DE}{CF}}{\frac{AE}{CF}}$=$\frac{\frac{AE}{BF}}{\frac{DE}{BF}}$,
即:$\frac{DE}{AE}=\frac{AE}{DE}$,
∴AE=DE,
(2)由(1)证得:$\frac{AE}{BF}$=$\frac{DE}{CF}$,$\frac{AE}{CF}$=$\frac{DE}{BF}$,
∴$\frac{\frac{AE}{BF}}{\frac{AE}{CF}}$=$\frac{\frac{DE}{CF}}{\frac{DE}{BF}}$,即$\frac{CF}{BF}$=$\frac{BF}{CF}$,
∴BF=CF.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
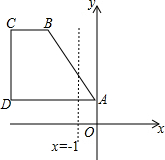 如图,已知四个点A(0,1),B(-3,4),C(-5,4),D(-5,1).
如图,已知四个点A(0,1),B(-3,4),C(-5,4),D(-5,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
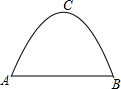 如图所示,某工厂大门是一抛物线形水泥建筑物,大门地面宽AB=4m,顶部C离地面高度为4m,现有一辆满载货物的汽车欲通过大门,货物顶部距离地面2m,装货宽度为2.5m,试判断这辆汽车能否顺利通过大门?通过计算说明.
如图所示,某工厂大门是一抛物线形水泥建筑物,大门地面宽AB=4m,顶部C离地面高度为4m,现有一辆满载货物的汽车欲通过大门,货物顶部距离地面2m,装货宽度为2.5m,试判断这辆汽车能否顺利通过大门?通过计算说明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
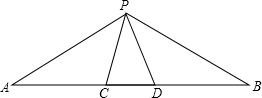 如图,点C,D在线段AB上,P是直线AB外一点,连接PA,PB,PC,PD.已知△PCD是等边三角形,如果CD2=AC•DB,求∠APB的度数.
如图,点C,D在线段AB上,P是直线AB外一点,连接PA,PB,PC,PD.已知△PCD是等边三角形,如果CD2=AC•DB,求∠APB的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com