
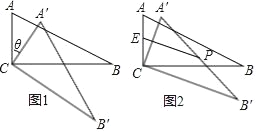
【题目】在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得到△A'B'C.
(1)如图1,当AB∥CB'时,设A'B'与CB相交于点D,求证:△A'CD是等边三角形.
(2)若E为AC的中点,P为A'B'的中点,则EP的最大值是多少,这时旋转角θ为多少度.
【答案】(1)见解析;(2)见解析.
【解析】
(1)当AB∥CB′时,∠BCB′=∠B=∠B′=30°,则∠A′CD=90°﹣∠BCB′=60°,∠A′DC=∠BCB′+∠B′=60°,可证:△A′CD是等边三角形;
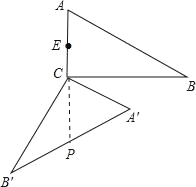
(2)连接CP,当E、C、P三点共线时,EP最长,根据图形求出此时的旋转角及EP的长.
(1)证明:∵AB∥CB′,
∴∠B=∠BC B′=30°,
∴∠BC A′=90°﹣30°=60°,
∵∠A′=∠A=60°,
∴△A′CD是等边三角形;
(2)如图,连接CP,当△ABC旋转到E、C、P三点共线时,EP最长,
此时θ=∠ACA1=120°,
∵∠B′=30°,∠A′CB′=90°,
设AC=a,
∴A′C=AC=![]() A′B′=a,
A′B′=a,
∵AC中点为E,A′B′中点为P,∠A′CB′=90°
∴CP=![]() A′B′=a,EC=
A′B′=a,EC=![]() a,
a,
∴EP=EC+CP=![]() a+a=
a+a=![]() AC.
AC.


科目:初中数学 来源: 题型:
【题目】如图,直线y=-![]() x+2
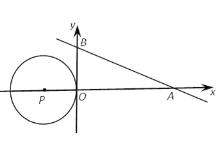
x+2![]() 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
A. 3 B. 4 C. 5 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点C、D在线段AB上,若点C是线段AD的中点,2BD>AD,则下列结论正确的是( ).
A. CD<AD- BD B. AB>2BD C. BD>AD D. BC>AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后回答问题.
①在进行二次根式的化简与运算时,我们有时会碰上如![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: ![]()
![]()
![]()
![]()
![]() 以上这种化简的步骤叫做分母有理化.
以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 ab2,ab 3 ,求 a2 b2 .我们可以把ab和ab看成是一个整体,令 xab , y ab ,则 a 2 b2 (a b)2 2ab x2 2y 4 610.这样,我们不用求出a,b,就可以得到最后的结果.
(1)计算:![]()
![]()
![]()
![]()
(2)已知 m 是正整数, a ![]() ,b
,b ![]() 且 2a2 1823ab 2b2 2019 .求 m.
且 2a2 1823ab 2b2 2019 .求 m.
(3)已知![]() ,则
,则![]() 的值为
的值为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
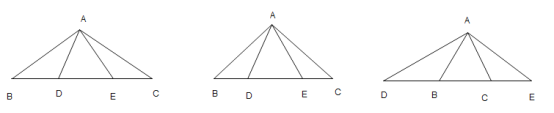
【题目】等腰直角三角形 ABC 中,BAC 90° ,AB AC 6 ![]() ,D,E 是线段 BC 上的动点,且 DAE 45°
,D,E 是线段 BC 上的动点,且 DAE 45°
(1)如图 1,请直接写出 BD,DE,EC 满足的关系式为 ,
(2)①如图 1, CE 3 ,请求出 ADE 的面积(写出过程);
②如图 2, EAC 30° ,请求出 CE 的长度(写出过程);
(3) 如图 3,D,E 运动到了线段的延长线上,且满足 DAE 135°,CE=8,直接写出 BD的长为
查看答案和解析>>
科目:初中数学 来源: 题型:
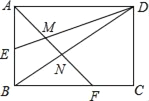
【题目】如图,矩形ABCD的边长AD=6,AB=4,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.
(1)求证:FB为⊙O的切线;
(2)若AB=8,CE=2,求sin∠F.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面从认知、延伸、应用三个层面来研究一种几何模型.
(1)如图,已知点E是线段BC上一点,若∠AED=∠B=∠C.求证 △ABE∽△ECD.

(2)如图,已知点E、F是线段BC上两点,AE与DF交于点H,若∠AHD=∠B=∠C.
求证:△ABE∽△FCD.

(3)如图,⊙O是等边△ABC的外接圆,点D是![]() 上一点,连接BD并延长交AC的延长线于点E;连接CD并延长交AB的延长线于点F. 猜想BF、BC、CE三线段的关系,并说明理由.
上一点,连接BD并延长交AC的延长线于点E;连接CD并延长交AB的延长线于点F. 猜想BF、BC、CE三线段的关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com